The Mathematics Magazine Pythagore a soixante ans. Cela est célébré avec un livre plein de penseurs. Le mathématicien Dirk Huylebrouck s'y est également aventuré. 'J'ai senti mon cerveau craquer à nouveau comme si j'étais jeune.'
Le Big Van Dale est l'un des dictionnaires les plus importants de la langue néerlandaise. À l'époque des correcteurs orthographiques, son importance diminue rapidement, tout comme sa notoriété. Il ne résistera peut-être pas à l'épreuve du temps, contrairement peut-être au Fat Pythagoras , un livre de plus de six cents problèmes mathématiques, dont certains datent de plusieurs milliers d'années. Dans le livre, bien sûr, ils ont une veste moderne.
Un des auteurs utilisera l'Eos- lecteur familier, de par ses blogs et ses articles :Paul Levrie, mathématicien à la Faculté des sciences appliquées de l'ingénieur de l'Université d'Anvers. Il est un collaborateur de longue date du magazine Pythagore , un concept mathématique aux Pays-Bas et en Flandre. Avec Jan Guichelaar, le membre le plus âgé du comité de rédaction du magazine, et Roosmarij Vanhommerig, le rédacteur en chef, il a réuni dans le livre les meilleurs penseurs qui ont travaillé à Pythagore au cours des soixante dernières années. sont apparus, entrecoupés d'innombrables amusements vous-savez-ça.
Quand j'ai demandé à Paul quel était son problème préféré, il a choisi "le nombre 148". Au-dessus de la question se trouvaient une boussole et trois points, dont deux noirs. Ils indiquaient respectivement le type de problème (un problème géométrique, dans ce cas) et le degré de difficulté :« Sur la figure, vous voyez un quadrilatère. Deux droites passant par les milieux de deux côtés opposés divisent le quadrilatère en quatre. L'aire de trois pièces est donnée. Quelle est l'aire du quatrième morceau ?'
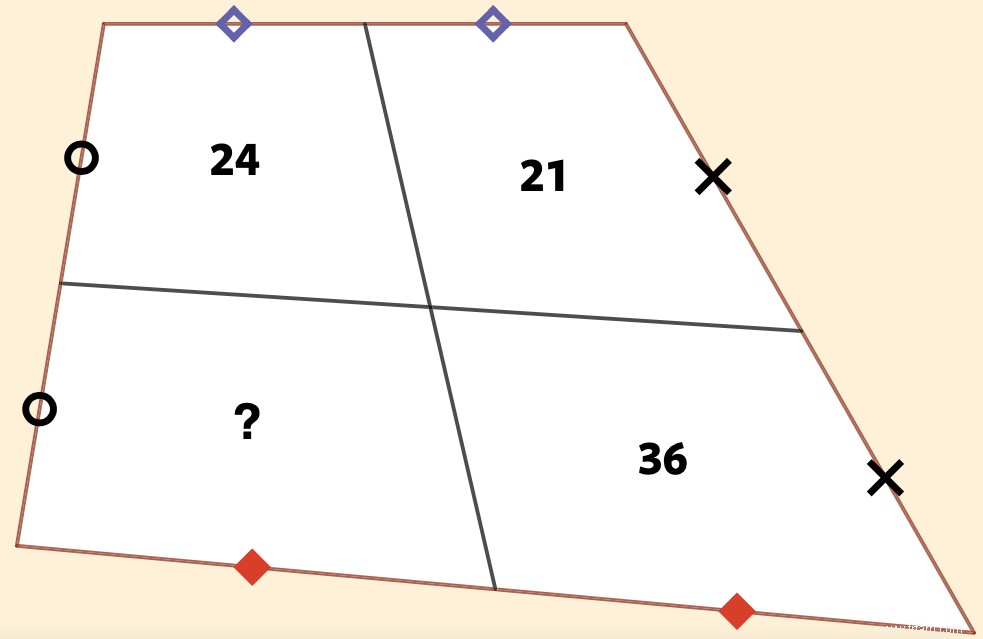
J'entends le lecteur penser :« Un mathématicien résout une telle chose immédiatement, n'est-ce pas ?» Mais je n'ai pas peur d'admettre que j'avais beaucoup de travail à faire moi-même ! J'ai senti mon cerveau craquer à nouveau comme si j'étais jeune. Un conseil :vous n'avez pas besoin de formules pour l'aire d'un quadrilatère, ni de théorème sur les quadrilatères. Le problème peut être résolu avec un seul dessin.
J'ai demandé à Paul pourquoi il avait choisi cette question. L'une de ses raisons était qu'il a une généralisation intéressante :"Prenez un quadrilatère", a-t-il dit, "et divisez chacun de ses côtés en un nombre pair de parties égales. Connectez ces points à l'aide d'une ligne au point correspondant sur le côté opposé. Si vous coloriez maintenant le résultat avec un motif en damier, la surface totale des carrés blancs est égale à la surface totale des noirs.'

Une bonne trouvaille, en effet, et cela illustre également comment vous pouvez inventer vous-même un théorème avec la créativité nécessaire.
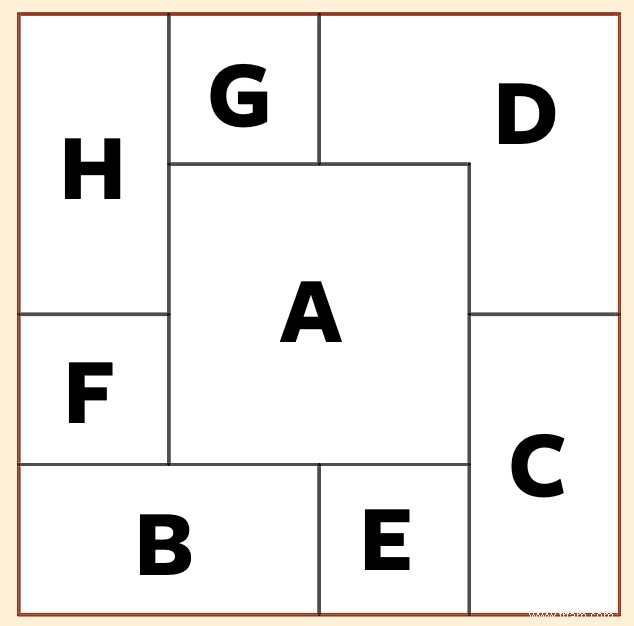
Tous les puzzles ne sont pas de nature géométrique ou arithmétique. Par exemple, il y a des 'énigmes' qui nécessitent une façon de raisonner différente et particulière (numéro 168 dans le livre) :'Huit feuilles de papier carrées, toutes de la même taille, sont placées une par une les unes sur les autres , se chevauchant toujours partiellement. Le résultat, un grand carré, est visible sur la figure. Pouvez-vous répertorier les feuilles de papier dans le bon ordre, de haut en bas ?"
Le livre illustre également bien que les mathématiques sont plus larges qu'on ne le pense généralement. Et, oh oui, même chaque numéro de page contient un défi. Par exemple, la page numéro 94 contient la combinaison – 1 × 1 + ((–2/2 + 3) × 3 + 4) × 4 + 55 et demande au lecteur de trouver une autre solution, en utilisant uniquement les chiffres 1, 1, 2 , 2, 3, 3, 4, 4 dans cet ordre. Il y a 299 pages numérotées, ce qui signifie 299 puzzles supplémentaires.
Les solutions aux énigmes de cette colonne se trouvent au bas de cette page.
Solution :Les quatre quadrilatères peuvent chacun être divisés en deux triangles, de sorte que les huit triangles résultants forment quatre paires, qui ont les mêmes aires deux à deux (base égale et hauteur égale). L'aire requise est (a+d) =(a+b) + (c+d) – (b+c) =24 + 36 – 21 =39.
Feuilles : A, D, G, H, F, B, E, C ; page :1 × 1 + 2 × 23 + 3 + 44 (par exemple).