Trois problèmes mathématiques bien connus sur la pizza, plus une blague qui compte pour 0,14.
A l'origine de cette affirmation se trouve la question :« Qu'est-ce qui est le plus, une pizza de 24 centimètres de diamètre, ou deux de 12 centimètres de diamètre ? » Eh bien, la grande a un rayon de 12 centimètres et donc une aire de pi fois 12 fois 12 soit environ 452 centimètres carrés. Le plus petit a un rayon de 6 centimètres et donc une superficie de 113 centimètres carrés. La surface de la grande pizza est donc d'environ 452/113 =4 fois plus grande que la plus petite. Il existe même un calculateur de pizza en ligne, qui tient compte de l'épaisseur de la croûte des grandes et des petites pizzas.
Vous mangez quatre fois plus sur une pizza avec un double jet.
Elle lit:"Si une pizza est divisée en huit morceaux coupés par le même point à des angles de 45 degrés, alors la somme des aires des morceaux alternés est égale." Notez qu'une roulette à pizza coupe toujours des lignes droites d'un bord à l'autre, contrairement à un couteau à tarte qui peut également faire des pointes sans couper toute la tarte. L'énoncé ne va pas de soi. Cela devient évident lorsque, par exemple, nous coupons quatre pièces en un certain point à des angles égaux de 90 degrés.
Le théorème vaut aussi pour douze, seize... pièces coupées par le même point à des angles égaux, c'est-à-dire de 30°, 22,5° respectivement... mais pas pour deux, quatre, six, dix, quatorze... pièces.
Bien qu'il puisse ressembler à l'un de ces théorèmes typiques de la Grèce antique d'il y a deux mille ans sur les cercles et leurs subdivisions, ce théorème a à peine cinquante ans. La preuve réelle de Greg Frederickson à l'université américaine Purdue, qui s'applique également à plus de huit pièces, n'a même pas dix ans.
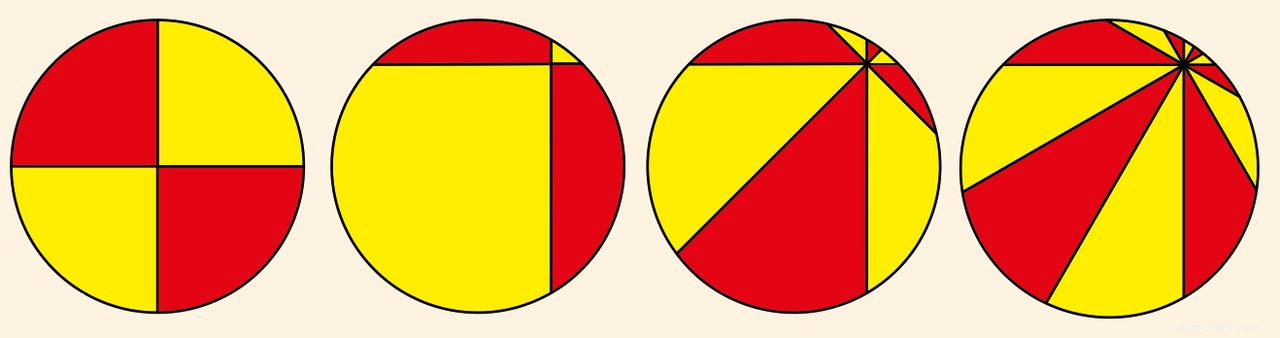
Dans le premier cas à quatre pièces, la somme des deux parties rouges est égale à la somme des deux pièces jaunes, dans le second cas elle ne l'est pas. Dans le troisième cas de huit pièces et le quatrième de douze pièces, la somme des parties rouges est égale à la somme des jaunes.
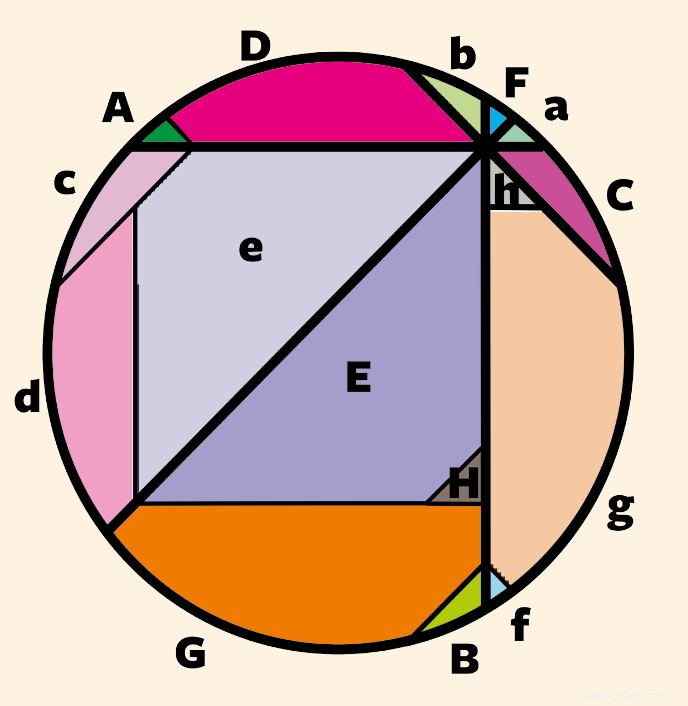
Une illustration de la preuve du théorème de la pizza pour la division donnée en huit morceaux :la somme des parties jaunes =a+b+c+d+e+f+g+h =A+B+C+D+ E+F+G+H =la somme des parties rouges.
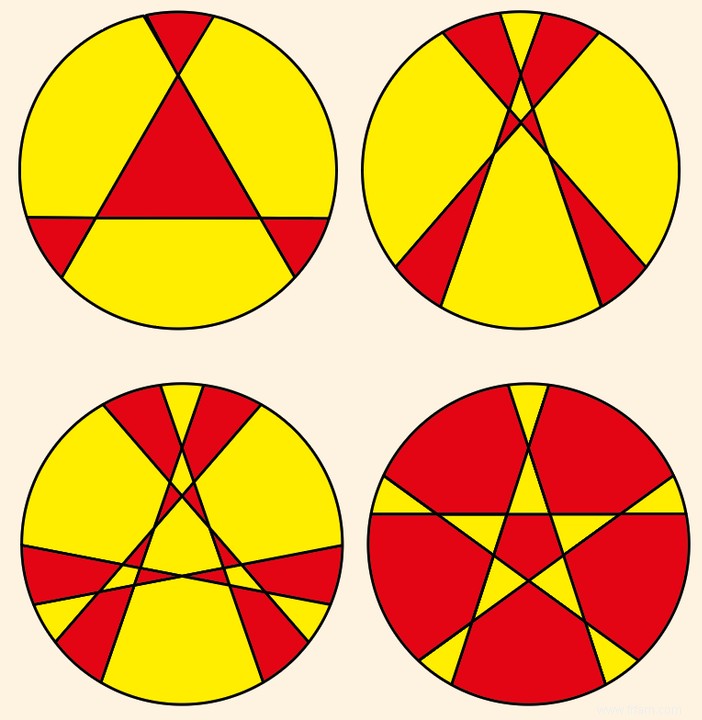
Un pizzaiolo paresseux veut obtenir le plus de morceaux possible en coupant le moins possible. Combien y a-t-il de pièces, si elles ne doivent pas nécessairement être égales ? Lorsqu'il coupe trois fois, il y a six morceaux - s'il coupe bien au même point qui n'est pas sur le bord de la pizza. Il y en a sept si ses trois intersections ne passent pas par le même point. Pour quatre coupes, cela peut aller jusqu'à onze, pour cinq seize. Et ainsi de suite :les numéros du 'traiteur paresseux' sont 1, 2, 4, 7, 11, 16, 22, 29, 37, 46, 56, 67, 79, 92, 106 ... Vous pouvez vérifier cela 'expérimentalement' si nécessaire.
Le nombre maximum de morceaux qu'une pizza peut couper en coupant trois, quatre, cinq ou six fois.
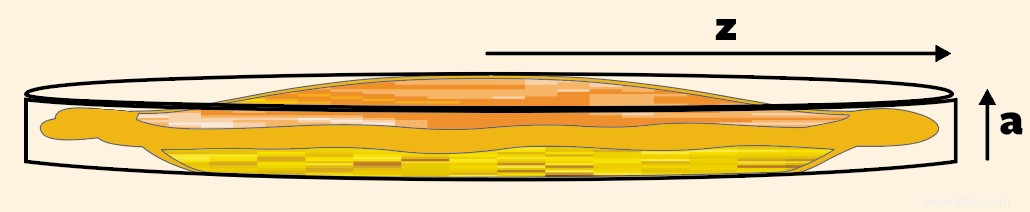
La réponse est une blague de geek standard :pi fois le rayon z fois le rayon z fois a ou pi.z.z.a.