Vous l'avez peut-être déjà entendu lors d'une récente réception du Nouvel An, peut-être par un collègue qui n'ose jamais vous parler pendant le travail normal :2017 est un numéro de pizza !
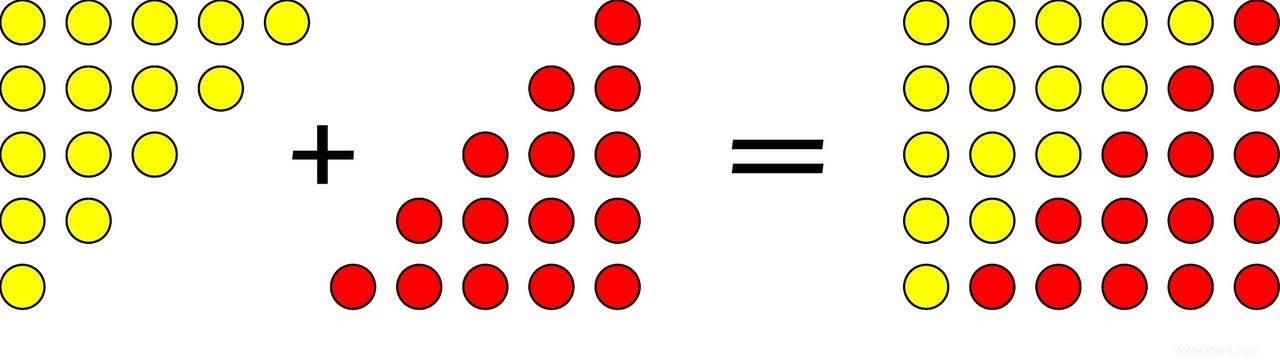
L'année dernière, le même collègue vous a dit que 2016 est un nombre triangulaire, après avoir bu du champagne trop rosé. J'espère que vous n'avez pas répondu cette année :"Beaucoup, un numéro triangulaire est toujours suivi d'un numéro de pizza", car alors vous avez bloqué le pauvre collègue des soirées du Nouvel An des dix prochaines années. La bonne réponse, bien sûr, est de poser la question :qu'est-ce qu'un numéro de pizza ? En tout cas, cela sonne moins sec qu'un nombre triangulaire, qui compte simplement le nombre de sphères dans un tas triangulaire. Vous trouverez ci-dessous les six premiers nombres triangulaires.
Une pile triangulaire avec 63 rangées, donc 63 sphères dans la rangée du bas, compte 2016 sphères. Le Nième nombre triangulaire TN peut être calculé rapidement grâce à la formule 2×TN=N×(N+1), qui se démontre sans mots ci-dessous :
Donc 2×T63 =63×64=4032. En plus de cette formule explicite pour obtenir TN pour calculer la relation de récurrence suivante est également très utile :
TN =TN−1 +N
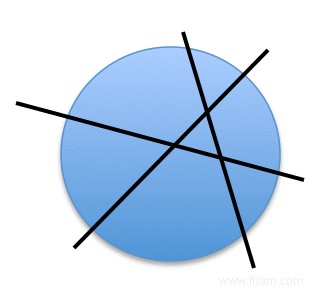
Cette relation dit simplement qu'une pile triangulaire avec N lignes formées par une pile plus petite avec N−1, rangées une rangée de N ampoules en bas. La prochaine année du nombre triangulaire est donc 2080 (2016+64). Un numéro de pizza PN n'a apparemment rien à voir avec ces nombres triangulaires, car PN montre le nombre maximum de morceaux dans lequel vous pouvez diviser une pizza (dépliée) par N coupes droites. C'est clair P1 =2 et P2 =4 † Avec trois coupes droites, vous obtenez généralement six morceaux, car dans une division classique, nous coupons toujours bien au milieu (de préférence avec des angles égaux, de sorte que nous obtenons six morceaux de taille égale), mais 6 n'est pas un numéro de pizza. Après tout, avec trois coupes droites, vous pouvez également obtenir 7 pièces, bien que de taille inégale :
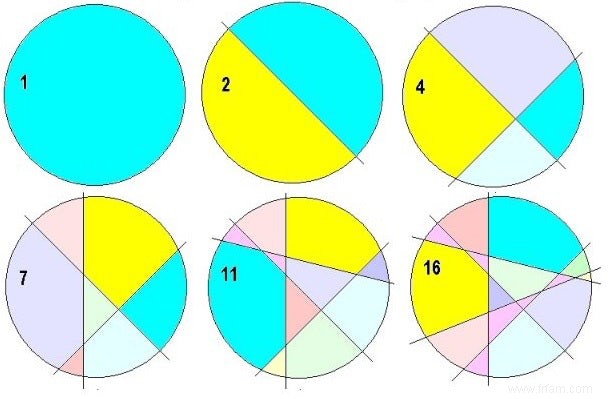
Puisque nous pouvons prouver mathématiquement que plus de sept morceaux échoueront avec trois coupes droites, 7 est le troisième numéro de pizza :P3 =7 † Ci-dessous, vous voyez les six premiers de la rangée de numéros de pizza, où nous P0 =1 (le zéro coupe donne en effet 1 morceau :la pizza entière).
Dans la vulgarisation des textes mathématiques, cette ligne est parfois appelée la ligne du traiteur paresseux (séquence du traiteur paresseux). En effet, avec ce découpage, le traiteur doit couper le moins possible pour obtenir le maximum de pièces. Quelques minutes (ou secondes ?) de réflexion convaincront le lecteur que la stratégie paresseuse (pour maximiser le nombre de pièces) consiste à laisser passer chaque intersection par une intersection sur deux sans passer par une intersection de deux autres intersections. Par exemple, regardez la pizza avec 3 intersections ci-dessus :aucune intersection ne contient une intersection des deux autres et chaque intersection rencontre également les deux autres. Si nous coupons maintenant une quatrième fois (pizza à côté), nous nous assurons simplement que cette nouvelle ligne de coupe croise les trois autres lignes de coupe. Parce que cette quatrième ligne est donc divisée en quatre intervalles par les trois autres, avec chaque intervalle une nouvelle ligne de partage dans les morceaux existants de la distribution précédente, cette quatrième coupe vient de diviser quatre morceaux existants (de la distribution précédente) en deux. La quatrième intersection donne quatre nouvelles pièces :P4 =P3 +4=7+4=11 † En général, nous voyons cette formule de récurrence pour les numéros de pizza :
PN =PN−1 +N
† Aha-expérience : les numéros de pizza correspondent à la même relation de récurrence que les numéros de triangle ! Mais comme T1=1 et P1=2, les numéros de pizza sont en avance d'un :
PN =TN+1 =N(N+1)2+1
Puisque T63=2016, P63=2017, est le nombre de tranches dans lesquelles un traiteur paresseux coupe sa pizza en 63 tranches. La prochaine année du nombre de pizzas ne sera pas avant 64 ans jusqu'en 2081, tout comme 2017 un nombre premier ! (Ceci est accessoire et soit dit en passant.) Ne nous demandez pas pourquoi, mais diviser les pizzas semble inspirer les mathématiciens. L'année dernière, des mathématiciens de l'Université de Liverpool ont trouvé une façon créative de diviser une pizza en morceaux égaux (extrêmement inadaptée aux traiteurs paresseux) :
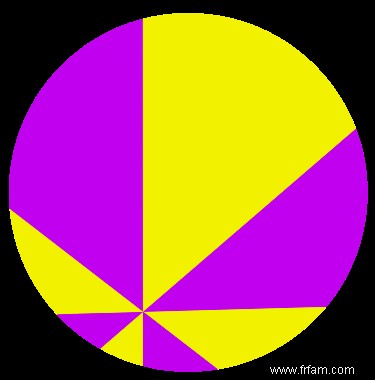
Et puis bien sûr il y a aussi le fameux pizza-Theorema † Une personne typique, non gênée par les connaissances en mathématiques, divise toujours une pizza en morceaux de taille égale (4 ou 6 ou 8 ou plus) en la coupant droit un certain nombre de fois, à travers le centre de la pizza, de sorte que tous les coins soient égaux. Ce centre de pizza est alors déterminé à vue, et à y regarder de plus près, il ne sera jamais exact. Mais le théorème de la pizza dit que ce n'est pas une mauvaise chose, du moins tant que vous parvenez à couper à angles égaux. THÉORME DE LA PIZZA : Supposons que vous divisez une pizza en n morceaux en coupant toujours par le même point (pas nécessairement le point central) et avec des angles de spline égaux (=360∘/n). Si n est un multiple de 4 et au moins 8, alors deux personnes prenant à tour de rôle un morceau (propre à côté du morceau précédent enlevé) auront mangé une surface de pizza égale à la fin. Dans l'exemple ci-dessous avec 8 pièces, la surface jaune totale est égale à la surface violette totale.
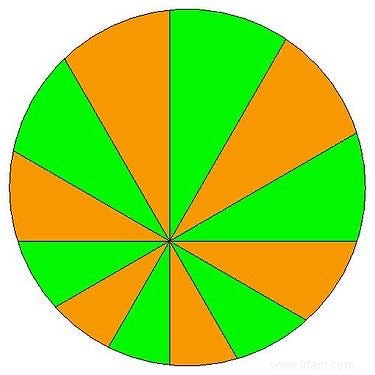
Toujours dans le cas avec 12 coins, la surface verte totale est égale à la surface orange totale :
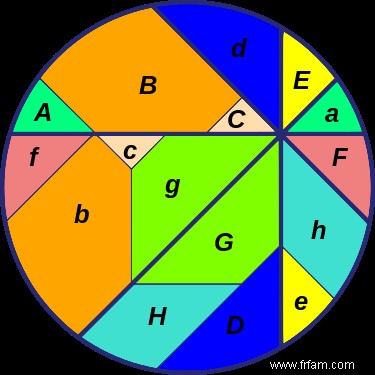
Cette déclaration est apparue pour la première fois dans un numéro d'une édition de Mathematics Magazine en 1968 (dissous par Goldberg). Mais nous préférons la preuve (pour 8 pièces) de 1994 par Carter and Wagon (sans paroles) :
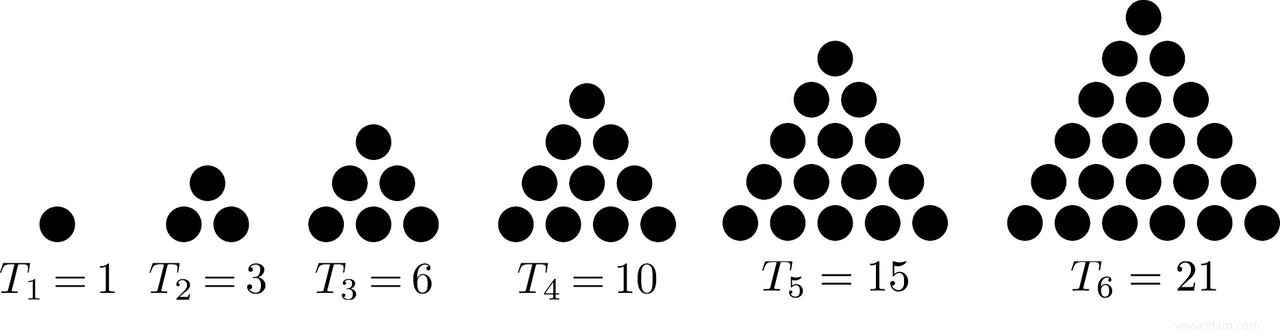
En 2012, Frederickson a généralisé cet argument purement graphique pour 12, 16, 20, ... pièces dans son article La preuve est dans la pizza † Nous avons également trouvé ce résultat dans un article de 1999 rédigé par cinq auteurs portant le nom de famille Hirschhorn. Dans la division du théorème de la pizza en n=4×k morceaux (avec k≥2), le résultat reste également valable pour k ètres, qui prennent à tour de rôle le coin suivant. Par exemple, si dans la division ci-dessus en 12 morceaux cette fois-ci trois convives prennent à tour de rôle un morceau adjacent, alors à la fin du trajet ils auront tous mangé la même quantité ! Nous pourrions continuer avec les mathématiques de la pizza jusqu'à ce que chaque lecteur soit frappé par l'indigestion, mais restons-en là.