Les mystères non résolus captivent l'imagination de chacun, qu'il s'agisse du Triangle des Bermudes, du monstre du Loch Ness ou, disons, de la disparition de Maddie McCann. La fascination persiste même lorsque le mystère s'est avéré être juste à l'improviste. Prenez le célèbre roman de science-fiction Le guide du voyageur galactique à partir de 1979, traduit en néerlandais par «Le manuel de l'auto-stoppeur transgalactique». Dans ce premier roman de ce qui allait devenir une série en cinq parties, l'auteur Douglas Adams écrit que la réponse à la question ultime de la vie, de l'univers et de tout est quarante-deux ("La réponse à la question ultime de la vie, de l'univers et de tout tout est en 42") † Un ordinateur ultra-puissant a calculé cela après plus de 7,5 millions d'années de calcul.
Les personnages se rendent compte que malheureusement cette réponse n'est pas très utile car la question n'a pas été formulée assez clairement et précisément. Afin de trouver la question concrète à laquelle 42 est la réponse, l'ordinateur dit qu'il devra construire une nouvelle version de lui-même et que cela prendra du temps. Cette nouvelle version de l'ordinateur s'avère être la Terre... et comment ça se passe, vous pouvez le lire dans les livres d'Adams.
Le choix du nombre 42 par cet auteur est un élément essentiel de la culture geek avec plein de blagues et de références au numéro avec un gros clin d'oeil. Demandez simplement à Google :"Quelle est la réponse à tout ?" Le premier hit est immédiatement 42. Cette réponse est également renvoyée à d'autres moteurs de recherche tels que Qwant ou Wolfram Alpha (spécialisés dans les problèmes de calcul mathématique), et à Cleverbot, un robot de chat intelligent.
En France, 42 est même le nom de tout un réseau d'établissements privés qui proposent des formations en informatique pour apprendre aux jeunes à programmer. Le « 42 Network » s'étend désormais jusqu'à Fremont, en Californie, au cœur de la Silicon Valley. Le nombre 42 apparaît également sous diverses formes dans le film Spider-Man :Into the Spider-Verse † Toute une liste de cas où le numéro apparaît peut être trouvée sur Wikipédia :voir la page néerlandaise pour '42 (number)', et surtout la page anglaise pour '42 (number)'.
Une petite sélection de celle-ci, où il est probablement inutile de découvrir quelle est la signification derrière :
Bien sûr, on a déjà demandé à Douglas Adams lui-même si le nombre 42 avait une signification particulière pour lui lorsqu'il a écrit le livre. Sa réponse donne à réfléchir:"Je l'ai juste choisi pour le plaisir. Je voulais un nombre banal, plutôt petit, et il s'est avéré. Représentations binaires, base 13, moines tibétains ... tout un non-sens complet. à l'extérieur pendant un moment, et a dit:"42, c'est bien." Je l'ai écrit. Fin de l'histoire."
42 est-il aussi un nombre spécial d'un point de vue strictement mathématique ?
Dans le système binaire, ou base 2, 42 s'écrit 101010, une séquence remarquablement simple. Pour de nombreux fans, c'était une raison suffisante pour organiser une fête le 10 octobre 2010 (10-10-10). La référence à la base 13 dans la réponse d'Adams a à voir avec le fait qu'à un moment donné dans le livre, il est dit que 42 est la réponse à la question :"Combien font 6 fois 9 ?". C'est absurde, bien sûr, car 6 × 9 =54 ... mais en base 13 le nombre écrit 42 est égal à 4 × 13 + 2 =54. Hormis les nombreux clins d'œil aux programmeurs de nombres pour s'amuser dans leur travail caché, et peu importe où nous rencontrons le nombre lorsque nous fouillons dans le monde ou dans l'histoire, la question demeure de savoir si 42 est aussi un nombre spécial d'un point de vue strictement mathématique.

Le nombre 42 a des propriétés mathématiques intéressantes. En voici quelques-uns :
• 42 est la somme des trois premières puissances impaires de deux (2 + 2 + 2 =42). La ligne a (n ) de sommes de puissances impaires de 2 est la ligne A020988 dans l'encyclopédie de Neil Sloane (https://oeis.org). En base 2 ça devient n- l'élément de cette ligne écrit 1010...10, où "10" n se répète, selon la formule a (n ) =(2/3)(4 – 1). Comme n augmente, la densité de ces nombres tend vers zéro, ce qui signifie que les nombres de cette ligne, dont 42, sont exceptionnellement rares.
• 42 est la somme des deux premières puissances de six (6 + 6 =42). La ligne b (n ) des sommes de puissance de 6 est la ligne A105281 dans l'encyclopédie de Sloane, définie par les formules b (0) =0 et b (n ) =6b (n – 1) + 6. La densité de ces nombres tend également vers 0 lorsque n monte.
• 42 est aussi un nombre catalan † Ces nombres ont été mentionnés pour la première fois - bien que sous un nom différent - par le mathématicien suisse Leonhard Euler, qui voulait comprendre le nombre de façons différentes d'obtenir un n Polygone convexe à côtés découpé en plusieurs triangles en reliant ses sommets par des segments. Cette ligne (A000108 par Neil Sloane) commence ainsi :1, 1, 2, 5, 14, 42, 132, ... La formule c (n ) =(2n )!/(n !(n + 1) !) renvoie le n -le terme de cette suite de nombres, dont la densité, comme celle des deux précédentes, est nulle à l'infini.
Les chiffres de la ligne c (n ) portent le nom du mathématicien franco-belge Eugène Charles Catalan (1814–1894), qui découvrit que c (n ) est le nombre de façons de n paire de parenthèses selon les règles habituelles d'écriture des parenthèses :une parenthèse n'est jamais fermée avant d'être ouverte, et ne peut être fermée que si toutes les parenthèses ouvertes ultérieurement sont fermées en premier.
Par exemple :c (3) =5, car trois paires de parenthèses peuvent s'écrire de cinq façons :
((())) ; † † † ()(()) † Les possibilités pour cinq paires de supports sont illustrées à la figure a.
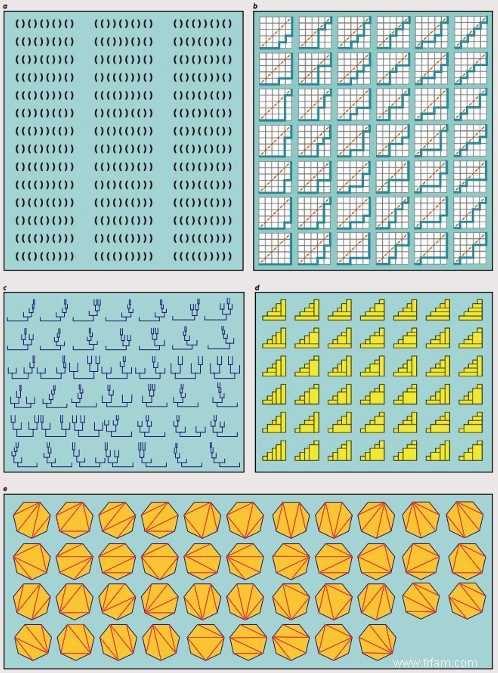
Le nombre c(n) est aussi le nombre de possibles non décroissants chemins pour connecter le coin inférieur gauche au coin supérieur droit dans un n à n maillage où la diagonale montante n'est pas dépassée (Figure b). Cette propriété permet d'utiliser le récursif définition de la séquence de nombres catalans pour comprendre c (0) =1 et c (n + 1) =Σc (k )c (n – k ), avec la somme prise sur tous les k s de 0 à n. En effet, pour supprimer tous les chemins (autorisés) dans un (n+1) à (n+1) grille, pour chaque chemin, nous considérons le point où il touche en premier la diagonale, après le départ dans le coin inférieur gauche, et définissons k égal au nombre de carrés (horizontaux ou verticaux) restant jusqu'au point final (k =0,…,n † Notez que le premier tronçon est un chemin non descendant sur un (n+1-k) à (n+1-k) grille qui stricte sous la diagonale (à l'exception des extrémités). Donc, cette première pièce reste un chemin légitime si nous omettons la première bride et la dernière bride verticale et remontons le tout d'une unité, mais maintenant dessiné dans un (n-k) à (n-k) la grille. Il s'ensuit que le nombre de premières pièces strictement en dessous de la diagonale est c(n-k). Les suites tiennent toujours dans un k à k grille (éventuellement tangente à la diagonale), et sont donc au nombre de c(k). La combinaison de toutes ces possibilités avec un k fixé donne donc le produit c(n-k)c(k) †
• 42 est un 'nombre pratique ', ce qui signifie que tout entier de 1 à 42 est la somme de ses diviseurs. Les premiers nombres pratiques sont :1, 2, 4, 6, 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 42, 48, 54, 56, 60, 64, 66, 72 (ligne A005153 de Neil Sloane). Il n'y a pas de formule simple pour le n -le terme dans cette série, et la densité des nombres cette fois ne tend pas vers zéro à l'infini.
C'est très beau et beau, mais on ne peut pas dire que 42 soit mathématiquement exceptionnel. Les numéros voisins 41 et 43 appartiennent également à de nombreuses lignes. Les propriétés de ces nombres et de nombreux autres peuvent être trouvées sur Wikipédia :allez à nl.wikipedia.org/wiki/42_ (number) et remplacez '42' par le numéro sur lequel vous souhaitez en savoir plus.
J'ai étudié avec mes collègues mathématiciens Nicolas Gauvrit et Hector Zénil ce qui rend un nombre intéressant ou banal. Nous avons utilisé les lignes incluses dans l'encyclopédie de Neil Sloane. D'une part, nous avons trouvé un lien théorique avec la complexité de Kolmogorov :plus la description minimale d'un nombre est longue, plus il est complexe (par exemple, la chaîne « abababababab » peut être décrite brièvement comme « 7 fois ab », ce qui ne peut pas être dit de la chaîne de même longueur 'x8r2y39gw5qh7n', qui est donc plus complexe). D'autre part, nous avons montré un effet culturel spécifique des nombres dans l'encyclopédie de Sloane, ce qui signifie que l'OEIS est donc également en partie basé sur des préférences humaines et non uniquement sur une pure objectivité mathématique.
Les informaticiens et les mathématiciens connaissent l'attrait du nombre 42, mais ont toujours cru qu'il était possible de faire de tels exercices avec n'importe quel autre nombre. Jusqu'à ce qu'un fait divers retienne leur attention :pour le nombre 42, le problème bien connu des "trois puissances" s'avérait beaucoup plus difficile à résoudre que pour tous les autres nombres inférieurs à 100.
La question est la suivante :quels entiers n peut être écrit comme la somme de trois cubes d'entiers, selon la formule n =un + b + c , et comment trouvez-vous un , b et c †
La difficulté – également pratique, pour effectuer des calculs – dans la détermination de ce trio est qu'il fait également intervenir des entiers négatifs. L'espace dans lequel on a , b et c doit chercher, est donc infini. C'est différent avec la somme des carrés :là, chaque carré a une valeur absolue inférieure à √n †
Des solutions de taille inattendue sont parfois trouvées pour le problème des puissances tierces, comme la solution pour 156, découverte en 2007 :
156 = 26577110807569 + (− 18161093358005) + (− 23381515025762).
Étonnamment, l'équation n =un + b + c pour certains entiers n pas de solution. Par exemple, c'est le cas pour tous les entiers n qui peut être exprimé par 9m + 4 ou 9m + 5 (par exemple 4, 5, 13, 14, 22, 23...). Cette affirmation est assez facile à justifier en utilisant le calcul « modulo 9 », qui suppose que 9 =0 et que seuls les nombres entre 0 et 8 ou entre – 4 et + 4 sont manipulés.
Cela donne :0 = 0 (mod 9); 1 = 1 (mod 9); 2 = 8 = – 1 (mod 9); 3 = 27 = 0 (mod 9); 4 = 64 = 1 (mod 9); 5 = (– 4) = – 64 = – 1 (mod 9); 6 = (– 3) = 0 (mod 9); 7 = (– 2) = 1 (mod 9); 8 = (– 1) = – 1 (mod 9).
Autrement dit :en modulo 9, le cube d'un entier est soit – 1 (=8), soit 0, soit 1. Alors toutes les sommes possibles de trois nombres sont choisies parmi 0, 1 et – 1 :
0 = 0 + 0 + 0 = 0 + 1 + (– 1); 1 = 1 + 0 + 0 = 1 + 1 + (– 1); 2 = 1 + 1 + 0 ; 3 = 1 + 1 + 1 ; 6 = – 3 = (– 1) + (– 1) + (– 1); 7 = – 2 = (– 1) + (– 1) + 0 ; 8 = – 1 = (– 1) + 0 + 0 =1 + (– 1) + (– 1).
Le résultat n'est jamais 4 ou 5 (=–4). Par conséquent, tout nombre pouvant s'écrire 9m + 4 ou 9m + 5 exclus comme résultat de la somme de trois cubes. Nous appelons cela des "valeurs interdites".

Pour illustrer à quel point il est difficile de comparer les n =un + b + c pour résoudre, regardons la situation pour n =1 et n =2.
Pour n =1 existe-t-il la solution évidente 1 + 1 + (– 1) =1.
Mais ce n'est pas le seul, car :
9 + (– 6) + (– 8) =729 + (– 216) + (– 512) =1.
Et en 1936, le mathématicien allemand Kurt Mahler proposa même une infinité de solutions. Pour tout entier p :
(9p 4 ) + (3p − 9p ) + (1 − 9p ) =1.
Le résultat peut être prouvé via l'identité remarquable :
(A + B ) =A + 3A B + 3AB + B †
Aussi pour n =2 il s'avère qu'il existe une infinité de solutions, ce qui a été prouvé en 1908 par le mathématicien A. S. Werebrusov. Pour tout entier p :
(6p + 1) + (1 − 6p ) + (− 6p ) =2.
En multipliant chaque terme de ces équations par le cube d'un entier (r ) on peut en déduire qu'il existe aussi une infinité de solutions pour chaque troisième puissance d'un entier et ses deux temps.
Prenons maintenant le nombre 16, deux fois le cube de 2. Cela donne :14 + (– 10) + (– 12) =16.
Pour n =3 , en revanche, seules deux solutions étaient connues en août 2019 :
1 + 1 + 1 =3 et 4 + 4 + (– 5) =3.
Alors bien sûr la question se pose :existe-t-il une solution pour toutes les valeurs non interdites de n †
Pour répondre à cette question, les mathématiciens ont commencé à étudier les valeurs non interdites une par une. Il s'agit de la ligne A060464 de Neil Sloane, qui commence par 1, 2, 3, 6, 7, 8, 9, 10, 11, 12, 15, 16, ... Si aucun des cas étudiés ne s'avère impossible, on peut raisonnablement supposons que pour tout entier n qui ne peut pas être exprimé par 9m +4 ou 9m +5 solutions existent pour l'équation n =un + b + c †
À mesure que la puissance de calcul des ordinateurs et des réseaux informatiques augmente, de plus en plus de résultats sont trouvés pour les nombres de cette ligne. Et nous revenons donc à ce fameux et intrigant nombre 42.
En 2009, Andrea-Stephan Elsenhans et Jörg Jahnel, utilisant une méthode proposée par Noam Elkies en 2000, ont analysé tous les triplés (a , b et c ) avec une valeur absolue allant jusqu'à 10 pour trouver des solutions pour les valeurs de n entre 1 et 1000. La publication de leurs résultats a montré qu'il existait une solution pour presque tous les nombres inférieurs à 1000, sauf pour quatorze nombres (33, 42, 74, 114, 165, 390, 579, 627, 633, 732, 795 , 906, 921 et 975).
Parmi les nombres inférieurs à 100, seuls trois sont restés non résolus :33, 42 et 74.
En 2016, le Néerlandais Sander Huisman a trouvé une solution pour 74 :(-284650292555885) + (66229832190556) + (283450105697727). Ensuite, seuls 33 et 42 sont restés.
Effectivement, vous l'avez deviné :en mars 2019, Andrew Booker a fait la facture du numéro 33 :(8866128975287528)+ (− 8778405442862239) + (− 273611146880740). À partir de ce moment, le nombre de Douglas Adams était le dernier entier positif inférieur à 100 qui n'était pas connu pour être exprimé comme la somme de trois cubes d'entiers.
Si la réponse s'était révélée négative, cela aurait été une bonne raison de considérer 42 comme un nombre « mathématiquement spécial » :ce serait le premier nombre pour lequel une solution à cette équation semblait possible et pourtant n'a pas pu être trouvée, pour combien de puissance de calcul il a également été utilisé.
La réponse rédemptrice est venue en 2020, après un effort de calcul massif coordonné par Andrew Booker et Andrew Sutherland du Massachusetts Institute of Technology. Les ordinateurs individuels participant au réseau Charity Engine avaient combiné plus d'un million d'heures de travail, résultant en :
42 =(– 80538738812075974) + 80435758145817515 + 12602123297335631
Des solutions ont également été récemment trouvées pour 165, 795 et 906. Par exemple, de tous les entiers inférieurs à 1000, seuls 114, 390, 579, 627, 633, 732, 921 et 975 restent non résolus.
La conjecture qu'il existe des solutions pour toutes les valeurs de n qui ne peut pas être exprimé par 9m + 4 ou 9m + 5 semble donc se confirmer. En 1992, Roger Heath-Brown est même allé plus loin en déclarant que toutes les valeurs non interdites de n peut être écrit de manière infinie comme la somme de trois cubes. Il reste donc du travail à faire.
La difficulté du problème est si énorme que la question "Est-ce n la somme de trois cubes ?" peut ne jamais être complètement résolu. Après tout, il est possible qu'aucun algorithme, aussi intelligent soit-il, ne trouve jamais tous les cas possibles. C'est également le cas, par exemple, du "problème d'arrêt" :l'une des descriptions de tout programme informatique et une entrée donnée déterminent toujours si le programme finira par s'arrêter ou s'exécuter pour toujours? Alan Turing a prouvé en 1936 qu'un algorithme pour résoudre le problème d'arrêt pour toutes les paires d'entrées de programme possibles ne peut pas exister Mais contrairement à l'arrêt problème, notre problème avec les cubes est purement mathématique et simple à décrire. Si quelqu'un devait prouver que cette équation ne peut jamais être résolue pour un nombre donné, ce serait une excellente nouvelle.
Le nombre 42 a peut-être été un dur à cuire, mais ce n'était pas la dernière étape !