Je me souviens encore quand j'ai vu la lumière et décidé d'étudier les mathématiques. Ce moment d'appel a eu lieu au cours du mois de mai de l'année dernière SO. Pendant les cours de géométrie projective, j'ai été époustouflé par la beauté des sections coniques et par la manière sacrée dont elles étaient étudiées dans l'Antiquité classique par des dieux grecs tels qu'Euclide, Archimède, Pappos, mais surtout Apollonios.

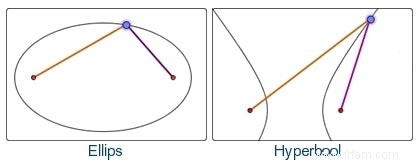
Pour ceux qui ne sont pas au courant, sections coniques est le nom collectif de 3 types de courbes mathématiques. Ellipses sont généralement dessinés à l'aide 2 points focaux † Pour chaque point de l'ellipse, est la somme des distances à ces foyers le même, c'est-à-dire égal au grand axe (distance entre les sommets principaux † Pour les points d'une hyperbole est la différence des distances jusqu'à ce que les 2 foyers soient alors à nouveau constants (aussi ici égal à la distance entre les sommets †
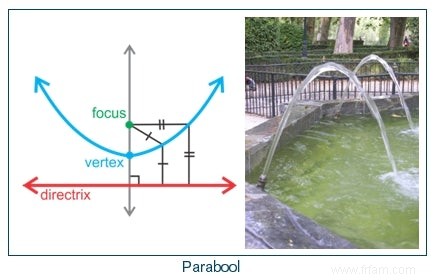
Ensuite, vous avez les paraboles qui jouent à peine un rôle dans cet article, mais fonctionnent glorieusement ailleurs, par exemple en tant que trajectoires de projectiles, télescopes spatiaux ou antennes paraboliques.
Les noms ellipse, hyperbole et parabole on le doit à Apollonius, qui termina son étude de ces courbes vers 225 av. écrit en Konika , l'un des chefs-d'œuvre les plus impressionnants de l'Antiquité, une collection de 8 manuscrits. La dernière partie a malheureusement été perdue, peut-être un point d'entrée pour un nouveau mystère de Dan Brown. De Konika, nous apprenons également qu'Apollonius a immédiatement eu la bonne perspicacité pour étudier ces courbes dans un contexte commun, à savoir en tant que différentes sections planes du même cône (circulaire), d'où le nom de famille sections coniques † Sur la figure, nous voyons que du point de vue d'un spectateur regardant dans le sommet du cône dans la direction de l'axe, chaque section conique apparaît essentiellement optiquement comme un cercle. Nous y reviendrons dans un instant. Ci-dessous, vous pouvez également voir un beau résultat d'un menuisier qui s'est inspiré du cône d'Apollonius.
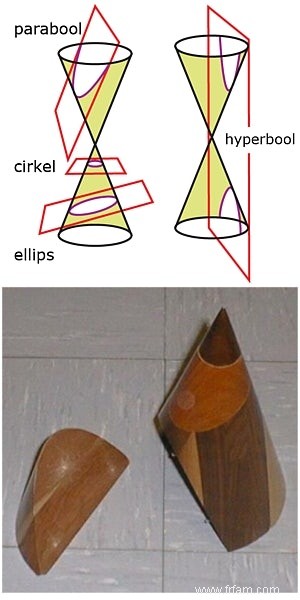
En aparté, nous nous référons ici au film Agora, dans lequel nous voyons comment Hypatie d'Alexandrie étudie passionnément ce modèle en bois pour les sections coniques. Hypatie est la première femme mathématicienne que nous ayons documentée historiquement. En l'an 415, elle fut écorchée vive et brûlée par des chrétiens radicalisés alors qu'elle voulait sauver des documents scientifiques de la bibliothèque d'Alexandrie de l'incendie. Qu'elle ait délibérément choisi "le mariage avec la vérité" plutôt qu'un mari ou un dieu ne l'aura pas aidée non plus.

Lorsque je parcours internet avec une des sections coniques comme terme de recherche, je découvre toujours un nouveau bien, la source semble inépuisable. Même si je dois avouer qu'à mon âge j'oublie parfois des choses que je connaissais autrefois, ce qui ajoute au plaisir de la découverte. Par exemple, j'ai récemment "découvert" qu'au sein de la grande famille des sections coniques, chaque ellipse individuelle a un lien particulier avec une hyperbole spécifique. On pourrait dire qu'ils forment un couple parfait, car ils se voient comme un cercle parfait, c'est-à-dire deux anneaux spirituels, qui, contrairement aux anneaux matériels, ne sont jamais perdus, jamais accrochés ou jamais secrètement enlevés. Voici un exemple d'un tel couple parfait :
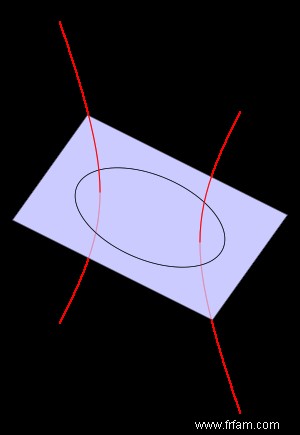
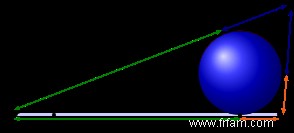
L'hyperbole est tracée dans le plan perpendiculaire au plan de l'ellipse et passant par le grand axe. Dans cette «étreinte étroite», les sommets de l'hyperbole se trouvent aux foyers de l'ellipse, et les sommets principaux de l'ellipse se trouvent aux foyers de l'hyperbole. Les points de l'hyperbole sont exactement les positions spatiales en dessous desquelles l'ellipse donnée est vue comme un cercle (et vice versa). Pour les experts :si la forme de l'ellipse est déterminée par l'excentricité e, alors son partenaire hyperbolique a une excentricité 1/e † On pourrait donc dire que la lampe sur la photo ci-dessous est située sur "l'ellipse partenaire" de la lumière hyperbolique, car elle voit cette lumière à travers l'ouverture circulaire de l'abat-jour.

Si vous voulez savoir pourquoi ce couple se voit effectivement comme un cercle, lisez un peu plus loin pour vous familiariser avec les ampoules de Dandelin † Je ne me souviens pas avoir entendu parler de cela à l'école ou à l'université, et avoir pêché moi-même ce joyau par la suite. Cependant, ce résultat est connu à l'étranger sous le nom de Belgian Stelling (donc un peu la Patrasche des mathématiques).

Germinal Pierre Dandelin est né en 1794 d'un père français et d'une mère belge. Il combattit pour les Français sous Napoléon, servit dans l'armée hollandaise sous le prince Bernhard et, en 1830, se tint en première ligne pendant la révolution belge. Son ami, le scientifique gantois Adolphe Quételet, avec qui il a écrit de la musique ensemble, a reconnu son talent mathématique et l'a aidé à trouver des emplois (non militaires) plus intéressants, allant d'astronome et professeur de physique à ingénieur des mines. Dandelin était particulièrement immortel par le résultat ci-dessous sur les sphères et les sections coniques. Quételet a probablement aussi eu une influence importante dans ce résultat, qui est donc parfois appelé la « thèse des Belges ». Si un plan coupe un cône, alors les sphères de Dandelin en question touchent le cône et le plan d'intersection en même temps :
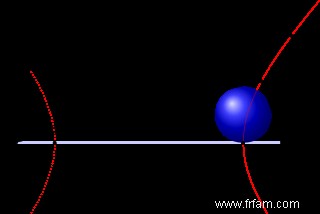
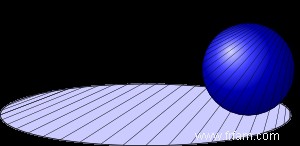
Si le plan coupe le cône dans une parabole, alors il n'y a qu'une seule sphère tangente simultanément. Dans la figure suivante, vous voyez une telle parabole, comme l'ombre projetée par une sphère sur un plan. La source lumineuse est à la même hauteur que le point le plus haut de la sphère. Le cône en question a pour sommet la source lumineuse et est tangent à la sphère dessinée. Dans ce cas, l'excentricité est e =1, donc la conique partenaire est à nouveau une parabole. A partir des points de cette deuxième parabole, vous voyez le bord de l'ombre comme un cercle. Et parce que nous savons que cela semble très improbable, nous avons tracé le cercle approprié dans la figure suivante.
La découverte ci-dessus de Dandelin a donné un aperçu renouvelé et des preuves élégantes des résultats classiques d'Apollonius. En effet, les points de contact des sphères avec le plan d'intersection sont précisément les foyers de la conique concernée (et pour les connaisseurs :le plan passant par le cercle tangent d'une sphère rencontre le plan d'intersection dans la directrice de cette section conique). Maintenant, à titre d'exemple, trouvons les points spatiaux à partir desquels vous voyez une ellipse donnée comme un cercle. Ce spectateur est donc au sommet d'un cône circulaire, avec l'ellipse en question comme section plate. Il est bien sûr vrai que l'illusion du cercle optique coïncide avec le cercle tangent, par exemple, de la sphère supérieure de Dandelin :
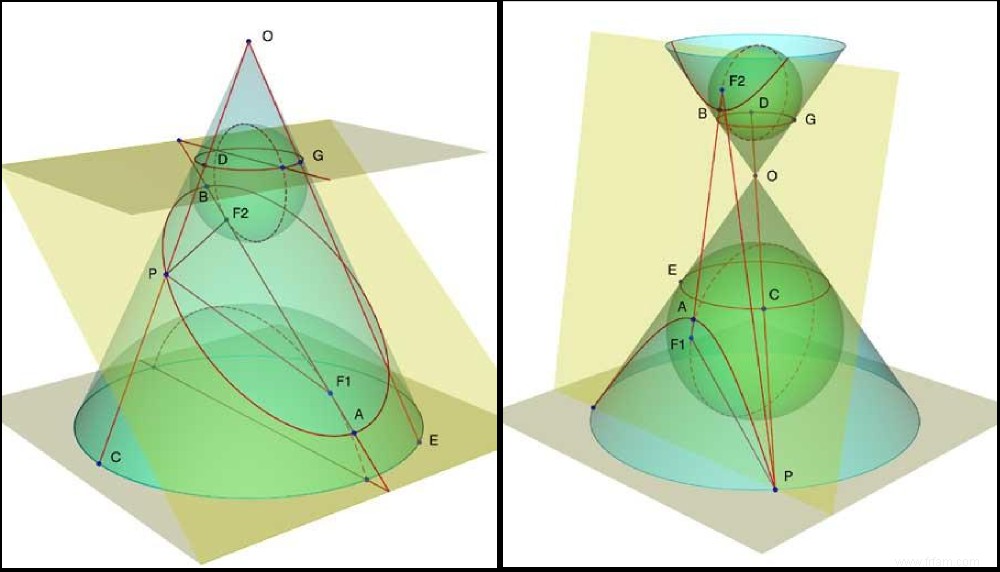
De plus, cette visionneuse (apex du cône) doit être dans le plan gamut perpendiculaire au plan de coupe et passant par le grand axe de l'ellipse (exercice pour lecteur motivé). Nous pouvons maintenant continuer notre raisonnement dans le plan gamma avec l'intersection suivante avec le cône et la sphère de Dandelin :

$\sf T$ est le sommet du cône. Les tangentes de $\sf T$ au cercle coupent l'ellipse, que nous voyons de côté comme un segment, aux sommets $\sf H_1$ et $\sf H_2$. $\sf F_1$ et $\sf F_2$ sont les foyers de l'ellipse. Le cercle est tangent à l'ellipse au foyer $\sf F_2$, dit Dandelin. Notez que les flèches de couleur similaire dans le dessin ci-dessus ont la même longueur en raison de la symétrie du cercle. Par conséquent, la distance entre $\sf T$ et $\sf H_1$ moins la distance entre $\sf T$ et $\sf H_2$ est égale à la longueur de la flèche verte moins la longueur de la flèche orange , et celle-ci est exactement égale à la distance entre les deux foyers de l'ellipse. Donc, si nous rétrécissons ou agrandissons maintenant le cercle de telle sorte qu'il continue de toucher l'ellipse à $\sf F_2$, et nous supposons que les tangentes de $\sf H_1$ et $\sf H_2$ au cercle se coupent en un point $\sf T'$ :
alors la distance de $\sf T'$ à $\sf H_1$ moins la distance de $\sf T'$ à $\sf H_2$ sera à nouveau égale à la distance entre les deux foyers de l'ellipse. Par la définition d'une hyperbole, nous pouvons conclure que tous les $\sf T$ possibles sont situés sur une hyperbole dont les foyers sont $\sf H_1$ et $\sf H_2$. Il est clair que cette hyperbole passe par $\sf F_2$, et les foyers de l'ellipse sont donc les sommets de cette hyperbole.