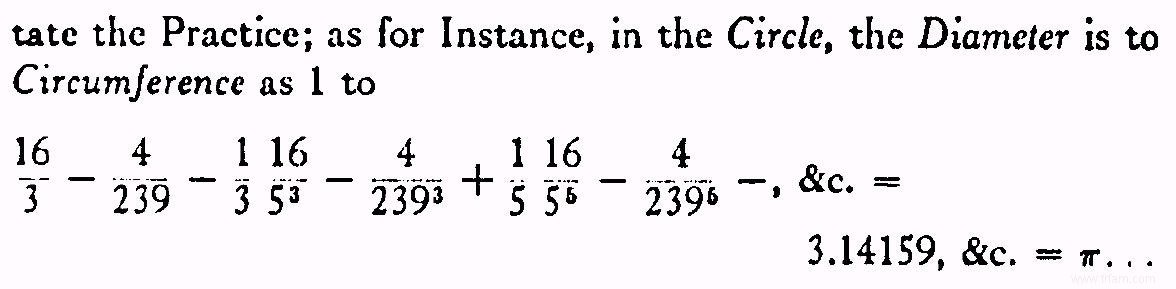Journée Pi - la version longue

Un aperçu de 10 ans de faits pi.

Il est clair qu'il y a quelque chose à célébrer le jour $\pi$ chaque année. Mais aujourd'hui, 14 mars 2019, plus que d'habitude :c'est aujourd'hui que démarre la Plateforme Wiskunde Vlaanderen, qui vise à unir la communauté mathématique en Flandre et à lui donner plus de visibilité. Vous pouvez en savoir plus sur le site Web :wwww.platformwiskunde.be. Si vous surfez là-bas, avec un peu de chance, vous finirez par revenir ici, où nous vous donnerons tout un tas de faits sur le nombre $\pi$ et $\pi$-jour pour votre divertissement.

Saviez-vous que :

• $\ldots$ est-ce $\pi$ jour aujourd'hui ? Pourquoi? Parce que la date du 14 mars est écrite dans l'orthographe américaine comme 3/14 et 3.14 est une approximation pour le nombre $\pi$.

• $ $ \ Ldots le nombre $ \ $ pi est jusqu'à 500 chiffres après la virgule décimale est égale à:
  3,14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127372458700660631558817488152092096282925409171536436789259036001133053054882046652138414695194151160943305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194913

• $\ldots$ donne au nombre $\pi$ le rapport de la circonférence d'un cercle à son diamètre ? Ou de l'aire d'un cercle au carré du rayon ?

• $\ldots$ vous pouvez également célébrer le nombre $\pi$ le 22 juillet, car 22/7 donne une approximation pour $\pi$ ? On appelle donc ce jour :jour d'approximation de pi.

• $\ldots$ l'inventeur du jour pi est un physicien ? Larry Shaw l'a lancé en 1988; ou, si vous ne le croyez pas
  
• $\ldots$ pi day n'est en fait pas un vrai jour férié mais a été inventé par des sociétés de mathématiques dans le but de pouvoir vendre plus de mathématiques ?
  
• $\ldots$ probablement la première fois que la notation $\pi$ est utilisée est dans le livre Synopsis Palmariorum Mathesos (1706) (traduit vaguement :une nouvelle introduction aux mathématiques) par un certain William Jones (1675-1749 ).

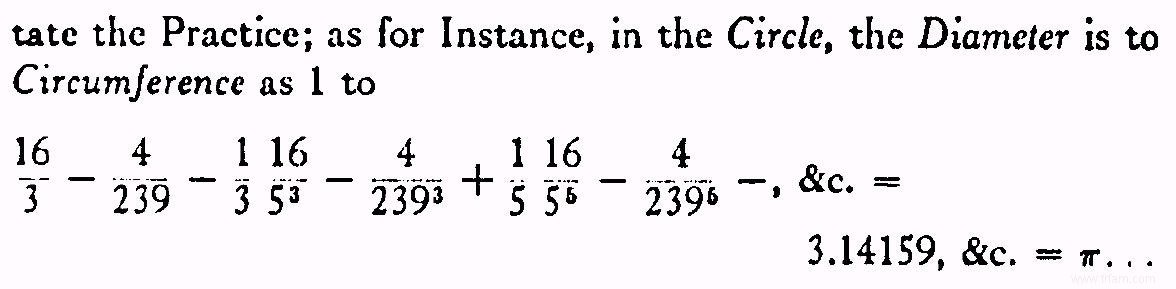
Le grand mathématicien Leonhard Euler (1707-1783) assura la diffusion de cette notation.

• $\ldots$ il n'y a absolument aucune régularité ou période dans les décimales du nombre $\pi$ ? Il n'y a donc pas de fraction avec numérateur et dénominateur entiers qui valent $\pi$. En conséquence, vous pouvez entrer dans le Livre Guinness des records avec le nombre $\pi$ (car les personnes sur la photo suivante qui détiennent le record dans la catégorie Avec le plus grand nombre de personnes forment le symbole du nombre $\pi$ -- 14 mars 2018).

• $\ldots$ le record du calcul du plus grand nombre de décimales de $\pi$ a été détenu jusqu'au 13 mars par Peter Trüb, qui a calculé $\pi^e$ billions de décimales de $\pi$ en 2016 ? Donc 22 459 157 718 361 chiffres. À ce jour, 14 mars, il appartient au développeur japonais de Google Cloud, Emma Haruka Iwao, qui a calculé 31 415 926 535 897 décimales (plus facile à retenir que le précédent record) dans le cloud. Le calcul a pris 121 jours. En savoir plus ici.
• $\ldots$ Archimède a déjà calculé des approximations pour le nombre $\pi$ vers l'an 250 av. Il l'a fait en partant d'un cercle de rayon 1 et en calculant la moitié de la circonférence de polygones réguliers inscrits et circonscrits avec un nombre croissant de côtés.

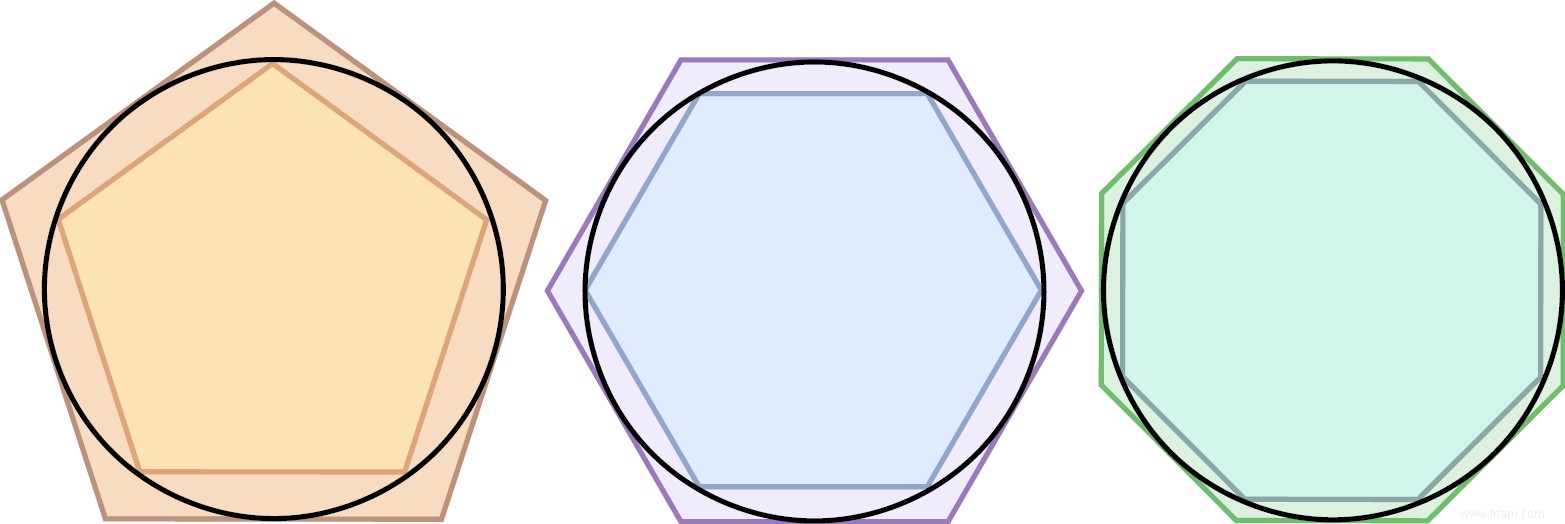
Ces valeurs fournissent des bornes vers le bas et vers le haut pour le nombre $\pi$. Le nombre $\pi$ devient donc parfois constante d'Archimède mentionné.

• $\ldots$ la formule la plus couramment utilisée pour calculer les décimales à partir de $\pi$ la formule de Machin (1706) est ? La voici :$$\frac{\pi}{4} =4 \cdot {\rm Bgtg} \frac{1}{5} - {\rm Bgtg} \frac{1}{239} $$ Cette formule peut être prouvé très facilement en utilisant nombres complexes (suit de $(5+i)^4=2(1+i) (239+i)$).
  
• $\ldots$ si on vous demande le jour $\pi$ combien de décimales de $\pi$ vous connaissez, la meilleure réponse est :tout, mais je travaille toujours sur la commande maintenant ?
  
• $\ldots$ les expressions exactes les plus anciennes avec lesquelles vous pouvez calculer le nombre $\pi$, sont les suivantes ?
  (1579) la formule du produit de Vieta $$ \frac{2}{\pi} \! =\textstyle\!\sqrt{\frac{1}{2}} \!\cdot\! \sqrt{\frac{1}{2} \!+\! \frac{1}{2} \!\cdot\! \sqrt{\frac{1}{2}}} \!\cdot\! \sqrt{\frac{1}{2} \!+\! \frac{1}{2} \!\cdot\! \sqrt{\frac{1}{2} \!+\! \frac{1}{2} \!\cdot\! \sqrt{\frac{1}{2}}}} \!\cdot\! \ldots $$
  (vers 1650) la formule du produit de Wallis $$ \frac{2}{\pi} =\frac{1\cdot 3}{2 \cdot 2} \cdot \frac{3 \ cdot 5}{4 \cdot 4} \cdot \frac{5 \cdot 7}{6 \cdot 6} \cdot \ldots $$
  (1655) la fraction continue de Lord Brouncker $$ \frac{4 }{ \pi} =1 + \cfrac[l]{1^2}{2+\cfrac[l]{3^2}{2+\cfrac[l]{5^2}{2 + \cfrac[ l] {7^2}{2 + \cfrac[l]{9^2}{\ldots}}}}} $$
  (vers 1670) la série de Gregory-Leibniz $$\frac{\pi } {4} =1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \ldots $$ (c'était en fait déjà connu vers 1400 par le mathématicien indien Madhava de Sangamagrama).
  
• $\ldots$ Ludolph Van Ceulen (1540-1610), mathématicien allemand, a passé une grande partie de sa vie à calculer (à la main) les décimales de $\pi$ ? Il l'a fait en utilisant la méthode d'Archimède et est arrivé à la 35ème décimale. C'est pourquoi $\pi$ est aussi appelé le nombre ludolfien.

• $\ldots$ cela a été imité par William Shanks (1812-1882), un mathématicien amateur britannique ? Il a calculé 20 ans à partir des 707 premières décimales. Il avait une routine régulière :calculer les décimales le matin, vérifier les calculs l'après-midi.
  
• $\ldots$ William Shanks avait fait une erreur à la 527ème décimale, et que le reste de ses calculs était également sans valeur ?
  
  Sept cent sept, Shanks a déclaré,
  Chiffres de $\pi$ qu'il calculait
  Et personne ne pouvait nier
  C'était un bon essai
  Mais il s'est trompé sur cinq vingt-huit.
  
  (auteur :N. Rose)
  
• $\ldots$ les 707 décimales calculées par Shanks en 1937 ont été peintes au plafond d'une des salles du Palais de la Découverte à Paris, et que les décimales incorrectes n'ont été corrigées qu'en 1947 ?

• $\ldots$ l'ingénieur japonais Akira Haraguchi connaît-il par cœur les 111700 premières décimales de $\pi$ ? En octobre 2006, il a annulé 100 000. Akira dit qu'elle ne fait rien de spécial le jour du $\pi$, sauf peut-être prendre des apéritifs un peu plus longs que d'habitude.
  
• $\ldots$ le nombre $$\frac{\ln (640\,320^3+744)}{\sqrt{163}}$$ est égal au nombre $\ à 30 chiffres après la virgule pi$ ?
  
• $\ldots$ un long métrage est sorti en 1998 avec le titre $\pi$?
  
• $\ldots$ dans l'état américain de l'Indiana la valeur du nombre $\pi$ en 1897 presque selon la loi est fixé à 3.2 ?
  
• $\ldots$ il y a beaucoup de mnémoniques pour aider à se souvenir des décimales de $\pi$ ? Par exemple :
  Comme j'ai envie d'un verre, alcoolisé bien sûr, après les lourds cours de mécanique quantique.
  
• $\ldots$ existe-t-il une forme poétique basée sur le nombre $\pi$ ? Voici un exemple (notez le nombre de lignes par strophe) par les Drs. P :
  
  Pi-sonnet
  
  Trois, un, quatre, un et cinq... se figer un instant ?
  Eh bien - vingt-deux puis, divisé par sept
  Exactement, c'est ce que je voulais dire :$\pi$
  
  Un Français voulait en faire un sonnet
  
  Cette série présente peu de symétrie
  Mais quatorze au total, c'est une donnée
  Deux lignes distinctes élevées en refrain -
  C'est comme ça que ça devient un poème, bien sûr et trois
  
  Jacques Bens a réussi à créer une nouvelle création de sonnet
  
  Qui ne serait pas fasciné par cela ?
  Après vingt ans, cela s'est bien terminé
  Dans notre langue. Vous devez être zélé
  Pour reprendre une telle innovation
  (Il l'appelait sonnet irrationnel)
  
• $\ldots$ qu'il y a des scientifiques qui pensent que $\pi$ est faux ? Ils veulent dire par là que c'était un mauvais choix de représenter le nombre $3,\!1415...$ avec l'abréviation $\pi$. Il aurait été plus logique d'indiquer le double, à savoir $6,\!2831$ avec la lettre $\pi$. Cela faciliterait déjà la lecture de l'horloge $\pi$ :à gauche, vous voyez la situation actuelle, à droite l'autre choix.

• $\ldots$ n'y a-t-il pas autant de séries infinies connues contenant $\pi^5$ dans la somme ? En voici deux :$$1+\frac{1}{2^{15}}\sum_{n=1}^\infty P(n) \frac{(n-1) !^{10}}{ \left (\frac{1}{2}\right)_{\!n}^5 \left(\frac{1}{2}\right)_{\!n+1}^5} =\frac {\ pi^5}{2^5}$$ et $$ 1-\frac{1}{2^5}\sum_{n=1}^\infty P(n) \frac{\left(\frac {1 }{2}\right)_{\!n-1}^5 \left(\frac{1}{2}\right)_{\!n}^5}{n!^{10}} =\ frac{2^5}{\pi^5}$$ avec $P(n)$ dans les deux séries égal à $1280n^8-640n^6+160n^4-20n^2+1$. Nous utilisons la notation de Pochhammer :$(a)_n=a\cdot (a+1)\cdots (a+n-1)$.

• $\ldots$ en attendant, nous savons aussi pourquoi exactement pi(e) est utilisé comme nom pour cette constante ?

• $\ldots$ en attendant on comprend aussi d'où vient le pi dans 'piano' ?

• $\ldots$ il existe de nombreuses approximations pandigitales pour $\pi$ ?
  Pandigital signifie que chaque chiffre de 1 à 9 apparaît exactement une fois. Voici un exemple. Le nombre $$3 + \frac{1-(9-8^{-5})^{-6}}{7+2^{-4}} $$ donne une approximation de $\pi$ allant jusqu'à 9 chiffres après la virgule sont corrects.
  (Notez qu'il existe une bien meilleure approximation pandigitale pour le nombre e :$$\left(1+9^{-4^{7\cdot 6}}\right ) ^{3^{2^{85}}} $$ est correct avec 18457734525360901453873570 décimales.)
  
• $\ldots$ dans le 21e épisode ("Margin in cuffs") de la quatrième saison de la série The Simpsons, le propriétaire du Kwik-E-Mart de Springfield Apu Nahasapeemapetilon au tribunal dit qu'il est capable Apu note en outre à juste titre que le Le 40 000e chiffre est égal à 1. Apparemment, les scénaristes de cet épisode ont préparé cette scène en demandant à la NASA quelle était la 40 000e décimale de $\ pi$, la NASA leur a ensuite envoyé une impression des 40 000 premiers chiffres.

• $\ldots$ la quadrature du cercle est-elle optiquement possible ? Pas de supercherie, juste un miroir.

Sans parler de l'expérience de l'aiguille de Buffon (un moyen fastidieux de trouver des approximations de $\pi$ à l'aide d'une aiguille et d'une feuille de papier avec des lignes), du mathématicien indien Ramanujan (qui avait un faible pour $\pi)$, le livre de 154 pages poème Poème Pi du groupe français Oulipo, le fait qu'avec le nombre $\pi$ on peut prouver qu'il y a une infinité de nombres premiers, et bien plus encore. Ce $\pi$ n'est pas seulement une invention de mathématiciens, mais se produit également dans la nature, vous pouvez le voir sur cette photo d'un s$\pi$innenorchis :

[]