La pénétration de cibles difficiles. Un cours accéléré en informatique quantique

Depuis le début de ce mois, nous savons grâce à Edward Snowden que la National Security Agency (NSA) des États-Unis a prévu un budget d'environ 80 millions de dollars pour son projet Penetrating hard Targets. Un objectif important de ce projet est de déchiffrer le cryptage commun du trafic Internet (codes RSA) et comprend des recherches fondamentales sur les ordinateurs quantiques.

Nous pouvons sembler gâtés maintenant, mais nous sommes habitués à des fuites plus spectaculaires ces derniers temps. Des chercheurs du monde entier tentent de déchiffrer des codes difficiles pour tester leur sécurité. Et l'ordinateur quantique est tout simplement un objet de recherche brûlant, on pourrait même parler d'une course universitaire pour être le premier à fabriquer une machine aussi efficace. Pour autant que nous sachions, la NSA est loin d'être en tête de cette course, plus proche que disons DARPA, la division de recherche de défense américaine, mais aussi plus proche que des institutions au Canada, en Russie, en Chine et en Europe, avec le QuTech Center récemment établi à Delft. comme l'un des acteurs les plus importants.

D'autre part, cette nouvelle a fait écho au mot "ordinateur quantique" lors des réceptions du Nouvel An, lors des pauses-café, dans des articles de journaux et des blogs attirant l'attention. Il est grand temps d'actualiser notre jargon en la matière, pour épater les collègues ou embellir les demandes de fonds.

Un cours intensif sur l'informatique quantique

• Les initiés affirment que l'horizon de production du premier ordinateur quantique d'utilisation pratique est d'environ quinze à vingt ans. Nous sommes donc bien à l'heure avec ce blog. D'autre part, les informaticiens s'affairent depuis deux décennies à concevoir des algorithmes pour ces futures machines. C'est précisément là que s'explique l'intérêt de la NSA et d'autres bailleurs de fonds pour les ordinateurs quantiques. A ce propos, souvenez-vous surtout :
  
  1. Algorithme de Grover :peut être utilisé pour rechercher des bases de données beaucoup plus rapidement que les logiciels existants pour les ordinateurs ordinaires. La plus grande implémentation actuelle de l'algorithme de Grover sur un prototype quantique ne peut traverser que des bases de données contenant huit données. Donc pour l'instant, notre vie privée n'est pas en danger, mais sachez que Google expérimente cet algorithme de recherche quantique dans ses laboratoires depuis plus de sept ans.
  2. Algorithme de Shor :Peter Shor, un professeur de mathématiques américain au MIT, a développé un algorithme de factorisation sensationnel pour les ordinateurs quantiques en 1994, en tant qu'employé des laboratoires Bell. Cet algorithme fonctionne beaucoup plus rapidement que les méthodes exponentielles des ordinateurs classiques. Cela nous obligera à l'avenir à revoir complètement le système de sécurité numérique actuel. En effet, la part du lion de notre trafic bancaire et Internet est cryptée par des codes RSA qui supposent qu'il est impossible d'en amorcer un grand nombre (d'une longueur d'environ 1024 bits) dans un délai raisonnable. De plus, cet algorithme était la bonne réponse au concours Physics Bowl dans l'épisode "The Bat Jar Conjecture" de la série télévisée The Big Bang Theory (voir photo).
     En 2010, des chercheurs ont créé un simple ordinateur quantique qui fonctionne avec des photons et ils ont réussi à exécuter l'algorithme de Shor à ce sujet. Ils ont réussi à factoriser 21 comme 7 $\fois 3 $. Le plus grand nombre, à notre connaissance, factorisé avec un logiciel quantique est 143 $ =11\fois 13 $ (en 2012, mais avec l'algorithme de factorisation adiabatique). Nous souhaitons à la NSA beaucoup de succès dans le crack de RSA-1024 avec ces moyens.
  3. Pour ceux qui veulent en savoir plus sur les algorithmes quantiques, et qui veulent même suivre le rythme, nous recommandons la page d'accueil de Stephen Jordan :Quantum Algorithm Zoo.

• En période difficile, nous sommes trop souvent bercés par la platitude selon laquelle chaque crise est une opportunité. En fait, dans cette histoire, l'obstacle qui a créé la crise s'est avéré être le levier de la nouvelle opportunité. Par exemple, nous sommes confrontés au diagnostic terminal pour la loi de Moore. Dans les années 1960, cet ingénieur d'Intel affirmait que le nombre de transistors dans un circuit intégré double tous les deux ans. Mais la densité de transistors sur une puce se heurte à une limitation physique. Au moment où les circuits de rétrécissement sont réalisés au niveau atomique, les règles de la mécanique quantique doivent être prises en compte. Le principe d'incertitude de Heisenberg rend les transistors à micro-échelle peu fiables. Richard Feynman , dans sa conférence à la première conférence sur la physique du calcul (1981), a suggéré d'utiliser cette incertitude comme principe d'un nouveau type d'ordinateur. Feynman est souvent appelé le père de l'ordinateur quantique (bien que le mathématicien russe Yu Manin ait déjà décrit un principe de calcul quantique en 1980, et que Paul Benioff soit parfois crédité comme le premier fondateur théorique).
  
• Mais avant même d'avoir fait son entrée, l'ordinateur quantique est déjà à l'origine de la prochaine crise en tant que menace potentielle pour notre vie privée et notre sécurité (algorithmes Grover et Shor). Mais là aussi, la mécanique quantique joue le double rôle de problème et de solution. Il constitue la base d'une nouvelle classe de codes, la cryptographie quantique, dont la distribution quantique de clés (QKD) est la plus connue. Selon ce principe, les messages sont codés dans des états quantiques de particules lumineuses, et dès que quelqu'un essaie d'intercepter et de lire le message, ces états quantiques sont détruits. Cette cryptographie ultra-sécurisée est déjà disponible dans le commerce et a même été utilisée pour sécuriser les élections suisses en 2007. En relation avec QKD se trouve le célèbre théorème de non-clonage en mécanique quantique. Selon ce théorème, il est impossible de copier un état quantique inconnu. Cela offre des opportunités sans précédent pour la sauvegarde des données et la protection des droits d'auteur.
  
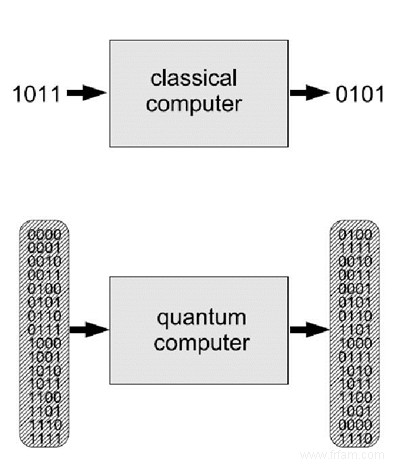
• Les ordinateurs classiques fonctionnent sur des bits, chacun pouvant prendre une seule des deux valeurs (off/on ou 0/1). L'unité d'information dans un ordinateur quantique est un qubit, un terme inventé par Benjamin Schumaker. Un qubit est l'état d'une particule élémentaire pour laquelle deux états observables peuvent être observés. Par exemple, le spin d'un électron ou la polarisation d'une particule lumineuse. On pourrait donc penser qu'un qubit contient les mêmes informations binaires qu'un bit normal. Mais le point de la mécanique quantique est que tant que nous n'observons pas ou ne mesurons pas une particule élémentaire, elle est dans un état quantique qui est la superposition de deux alternatives.
  
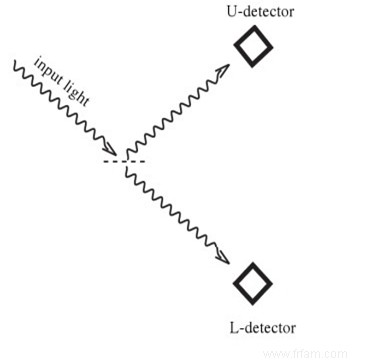
• Une illustration populaire dans les manuels de mécanique quantique est un miroir semi-transparent (séparateur de faisceau), indiqué ci-dessous par une ligne brisée. Seule la moitié de la lumière incidente passe à travers, l'autre moitié est réfléchie. Les deux faisceaux du faisceau lumineux dédoublé présentent donc la moitié de l'intensité d'origine. Jusqu'ici le tarif digeste, au niveau des observations quotidiennes.

• Mais supposons maintenant que nous atténuons l'intensité de la lumière incidente de telle manière qu'il ne reste qu'une seule particule élémentaire de lumière. Nous avons la technologie pour réaliser cela, et aussi pour détecter ce photon (par exemple avec un photomultiplicateur). Si l'on place deux de ces détecteurs au-delà du « demi-miroir », on peut décider du comportement de ce photon :transmission ou réflexion. Si nous répétons cette expérience plusieurs fois, les détecteurs de photons toucheront chacun environ la moitié du temps, comme prévu avec un miroir semi-transparent. Mais les gens se déplacent comme des éléphants maladroits entre les particules de porcelaine qui composent le monde. S'il y a deux possibilités (exclusives), par exemple la transmission (T) ou la réflexion (R), notre cerveau limité veut couper le nœud, mais secrètement un photon se comporte plus subtilement, à savoir dans un état mixte de T et R après avoir passé le séparateur de faisceau est passé.

• La logique quantique est donc radicalement différente de la logique binaire familière avec laquelle nous voulons habituellement comprendre le monde et sur laquelle les ordinateurs classiques sont basés. Supposons que l'on considère deux états possibles pour une particule lumineuse, selon qu'elle se déplace :vers le bas (1) ou vers le haut (0). Selon la logique de la perception humaine, après avoir rencontré la lame séparatrice, on retrouve un état binaire (0 ou 1). Par exemple, si un photon incident vers le bas réfléchit alors nous obtenons un mouvement vers le haut, le 0 a été converti en 1. Mais sans mesures humaines, le photon obéit aux lois quantiques, qui pour le séparateur de faisceau ressemble à ceci :
  $$ \gauche| 0\right\rangle \mapsto \frac{1}{\sqrt{2}}\left| 0\right\rangle -\frac{1}{\sqrt{2}}\left| 1\droite\rangle$$ $$ \gauche| 1\right\rangle \mapsto \frac{1}{\sqrt{2}}\left| 0\right\rangle + \frac{1}{\sqrt{2}}\left| 1\droite\rangle$$
• Le format $\left| 0\right\rangle$ ou $\left| 1\right\rangle$ fait référence aux états quantiques qui se produisent simultanément, chacun avec son propre poids $\pm 1/ \sqrt{2}$ (les amplitudes de probabilité), contrairement aux états binaires (observables) 0 et 1, qui se produisent exclusivement . (En aparté, cette notation étrange pour un état quantique est appelée un ket dans le jargon, et est la moitié droite de la notation de Dirac ou de la notation de frein). Nous n'expliquons pas comment calculer les bonnes valeurs pour les amplitudes de probabilité, qui sont parfois même des nombres complexes, ce sont des choses qu'on apprend dans un cours de mécanique quantique. Par définition, les carrés des amplitudes de probabilité doivent donner les probabilités de détection de l'état associé, et on peut le vérifier (selon le principe d'un miroir semi-transparent) :
  $$\left({\pm 1 / \ sqrt{2}}\right)^2 =\frac{1}{2}$$
• Lors de la récente présentation de la Golden Pipette, Lieven Scheire portait le T-shirt suivant. Nous en comprenons maintenant juste assez sur la mécanique quantique pour apprécier sa blague ringard :"Ne me demandez pas comment je me sens, si je pouvais m'effondrer."

• Depuis 2009, les premières véritables puces quantiques existent, mais avec des fonctionnalités modestes. Depuis 2011, la société canadienne D-Wave a même lancé la production commerciale d'un processeur de 128 qubits (le slogan sur leur site Web :Nous avons un problème avec l'impossible). En mai 2013, le nouvel ordinateur quantique de 512 qubits a été installé au prestigieux Quantum Artificial Intelligence Lab, une collaboration entre la NASA, Google et l'USRA.
  
• L'entrée pour un ordinateur classique peut être représentée par une rangée de $n$ bits, $011\ldots 01$, qui est un choix de $2^n$ possibilités. Mais une suite de $n$qubits représente une superposition de toutes ces $2^n$ possibilités ! Un ordinateur quantique (avec des portes quantiques) est ainsi capable d'effectuer des calculs super-parallèles simultanément sur toutes les entrées possibles de $n$ bits.

• Pour certains problèmes difficiles, tels que la factorisation des nombres naturels en facteurs premiers, la mise en place d'un horaire de cours ou le problème du voyageur de commerce, les algorithmes actuels nécessitent un nombre exponentiel d'opérations, mais les ordinateurs quantiques peuvent le faire beaucoup plus rapidement car ils peuvent considérer tous possibilités à la fois.
  
• Une puce classique contient des circuits logiques composés de circuits logiques tels que OU, ET et NON. Une porte quantique a des qubits comme entrées et sorties. Par exemple, le séparateur de faisceau mentionné ci-dessus réalise la porte dite d'Hadamard, qui n'a pas d'équivalent à une porte classique. Ce port a une entrée qubit et une sortie qubit. Un autre exemple important est la porte cNOT, une porte à 2 qubits qui, avec la porte Hadamard, est suffisante pour simuler la machine quantique universelle de Turing, telle que décrite par David Deutsch, et donc en principe suffisante pour tout calculer dans notre macro - et micro-monde.
  
• Dans la description mathématique, les états quantiques sont représentés comme des vecteurs dans un espace de Hilbert, et les portes quantiques comme des opérateurs unitaires dans cet espace. Mais avant que vous n'entamiez des noms à ce sujet pendant votre pause-café au travail, je ferais d'abord quelques recherches.
  
• Préparer des qubits peut être une prouesse technologique, mais le vrai défi dans la construction d'un ordinateur quantique est de maintenir les circuits quantiques isolés afin qu'ils n'interagissent pas avec l'environnement. Car dès que quelque chose peut être mesuré lors des calculs, dès que l'information fuit tôt, les états quantiques menacent de s'effondrer, entraînant des imprécisions. C'est ce qu'on appelle le problème de décohérence. Pour cette raison, les circuits des processeurs quantiques d'aujourd'hui sont fabriqués avec des supraconducteurs, et fonctionnent généralement à des températures proches du zéro absolu, ce qui limite évidemment son utilisation pratique.
  
• Dans ce contexte, le principe de Landauer de 1961 est très important. Chaque fois qu'un peu d'information est perdue lors d'un calcul informatique, une certaine énergie est libérée. L'oubli réchauffe. C'est le cas, par exemple, d'une porte ET, qui a deux entrées mais une seule sortie. Heureusement, les calculs quantiques utilisent des portes représentées par des opérateurs unitaires et sont par définition toujours réversibles.
  
• Outre le principe de superposition, responsable du parallélisme dans les ordinateurs quantiques, il existe un autre phénomène quantique qui joue un rôle dans ces machines futuristes :l'intrication quantique. Cela signifie que l'état quantique de deux particules élémentaires restera connecté même si elles sont séparées. Cela est nécessaire, par exemple, si l'on veut vérifier un calcul, ne serait-ce que pour voir s'il est terminé. A cause du problème de décohérence des ordinateurs quantiques (voir ci-dessus), nous devons laisser les ordinateurs quantiques faire leur travail dans des conditions parfaitement isolées, mais un jour nous aimerions connaître la réponse, bien sûr. Une solution théorique propose de contrôler les qubits indirectement, par des observations sur d'autres particules mais intriquées, afin que l'état quantique des qubits à l'intérieur de l'ordinateur quantique ne s'effondre pas.

Encore

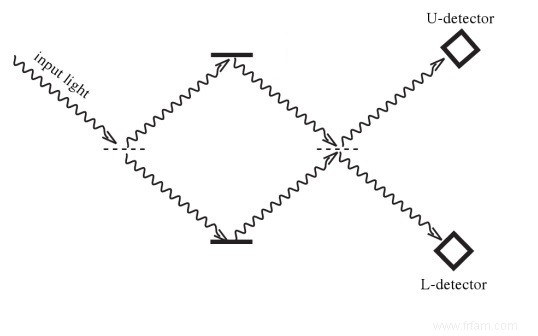
En prime, juste à côté de ce cours accéléré sur l'ordinateur quantique, une autre courte leçon de mécanique quantique. Comment les spécialistes quantiques savent-ils que les particules élémentaires, après un événement avec des résultats alternatifs, sont dans un état quantique parallèle. Après tout, à partir du moment où quelqu'un veut tester cela, à partir du moment où quelqu'un le regarde même, l'état quantique s'effondre pour montrer la couleur à un seul des résultats. Heureusement, une personne est assez intelligente pour mettre son propre cerveau de raisonnement logique classique hors jeu. Ci-dessous, nous laissons un photon passer deux séparateurs de faisceau sans aucune interférence et ne détectons qu'ensuite son état.

Les miroirs semi-transparents correspondent aux lignes pointillées, et les deux lignes pleines représentent des miroirs entièrement réfléchissants. Une particule lumineuse initialement dirigée vers le bas comme sur la figure peut « choisir » entre quatre trajectoires possibles :RR, RT, TR et TT, où R représente la réflexion et T la transmission au niveau des séparateurs de faisceau successifs. A noter que les trajectoires RR et TT montent dans la dernière partie de trajectoire et arrivent dans le détecteur du haut. D'autre part, les trajectoires RT et TR entraînent un mouvement vers le bas qui va taper contre le détecteur de photons inférieur. Si un photon nouait effectivement le nœud à chaque passage dans un demi-miroir, avec 50 % de chance pour chacune des deux possibilités, alors les quatre trajectoires (RR, RT, TR, TT) seraient également probables (25 % de chance chacune ). Si nous devions répéter cette expérience tout au long de la journée, nous nous attendons à ce que le soir les deux détecteurs aient mesuré approximativement le même nombre de photons. Mais ce n'est pas le cas :il s'avère que tous les photons sont détectés en haut (dans un mouvement ascendant), aucun en bas ! Ceci est parfaitement prédit par la mécanique quantique. Nous le montrons pour le photon incident vers le bas (comme sur la figure), associé à l'état de base $\left| 1\right\rangle$ :

Premier demi-miroir :
$$\left| 1\right\rangle \mapsto \frac{1}{\sqrt{2}}\left| 0\right\rangle + \frac{1}{\sqrt{2}}\left| 1\right\rangle$$
Miroir :
$$\mapsto \frac{1}{\sqrt{2}}\left| 1\right\rangle + \frac{1}{\sqrt{2}}\left| 0\right\rangle$$
Deuxième demi-miroir :
$$\mapsto \frac{1}{\sqrt{2}}(\frac{1}{\sqrt{2}}\ gauche| 0\right\rangle + \frac{1}{\sqrt{2}}\left| 1\right\rangle) + \frac{1}{\sqrt{2}}(\frac{1}{\ sqrt{ 2}}\left|0\right\rangle -\frac{1}{\sqrt{2}}\left|1\right\rangle)$$ $$=\left| 0\right\rangle$$

Astuce de lecture

Toujours debout après quinze ans (et toujours un plaisir à relire) :

Le processeur Feynman , par Gerard J. Milburn, Perseus Books, 1998.