Harvey Friedman se donne pour tâche de rendre tangibles les mathématiques inaccessibles. Plus tard cette année, le scientifique de renom occupera un poste de professeur invité à l'Université de Gand. Une conversation avec un homme aussi chaleureux qu'intelligent.
Harvey Friedman est un génie :à 18 ans, il obtient son doctorat en mathématiques au prestigieux Massachusetts Institute of Technology. Immédiatement après, il a été nommé à la non moins respectable université de Stanford. Depuis lors, il est dans le Livre Guinness des records du monde noté comme le plus jeune professeur de tous les temps.
Le professeur adjoint de philosophie de l'époque est devenu plus tard également professeur de mathématiques et de musique, jusqu'à sa retraite en 2012. Un an plus tard, il a reçu un doctorat honorifique de l'Université de Gand. Cette année, il décide de renforcer encore les liens avec l'Université de Gand :non seulement il deviendra professeur invité dans le groupe de recherche en logique mathématique d'Andreas Weiermann, mais il créera également une archive permanente où ses travaux pourront être consultés.
Le temps d'un chat. Mais comment, en tant qu'intervieweur, tenir tête à quelqu'un qui a un jour écrit un texte intitulé « Une preuve divine de la cohérence des mathématiques » ? Friedman y a montré que les mathématiques conventionnelles sont sans contradiction interne quand on accepte l'existence de Dieu. De plus, la participation de Friedman à des conférences a montré qu'il réfléchit très rapidement et pose immédiatement ses questions fondées.
C'est pourquoi j'ai été soutenu pour cette conversation par Weiermann lui-même, qui a également soumis des questions à Friedman. Il a produit une série de réponses informelles.
Pouvez-vous illustrer votre recherche en quelques phrases ?
« En mathématiques, vous posez des questions auxquelles vous voulez des réponses sans ambiguïté. Vous voulez savoir si vos affirmations sont vraies ou non. Mais dans les années 1930, l'Américain d'origine autrichienne Kurt Gödel (1906-1978, éd.) découvre qu'il y a des affirmations mathématiques que vous ne pouvez ni prouver ni réfuter. Ils sont totalement inaccessibles. Le travail de Gödel était plutôt abstrait et éloigné de la réalité mathématique. Le désir grandit de rendre son travail un peu plus terre à terre et de le relier à la réalité physique.'
"J'ai cherché ça pendant 54 ans. J'ai présenté des problèmes tangibles associés aux affirmations plus philosophiques de Gödel. J'ai formulé des problèmes mathématiques de tous les jours auxquels on ne peut pas répondre en mathématiques elles-mêmes (voir encadré 'Tous les jours et non résolus', éd.) .'
Cela ne vous déprime-t-il pas ? Le mathématicien russe Vladimir Arnold a déclaré un jour que la découverte de Gödel l'avait découragé pendant un certain temps.
Mais il y a aussi un côté positif ! Si vous étendez vos méthodes d'une manière que les mathématiciens n'ont pas encore généralement acceptée, vous pouvez toujours traiter et résoudre ces problèmes de Gödel. Que nous ayons découvert ces principes mathématiques supérieurs de cette manière me rend heureux.'
Le paradoxe du mille-pattes stipule que l'insecte réfléchit à la façon dont il parvient à marcher et c'est pourquoi il trébuche. De nombreux mathématiciens ne se soucient peut-être pas beaucoup de ces paradoxes selon Gödel et continuent simplement leur travail ...
« Je dois vous interrompre un instant. Il ne s'agit pas de paradoxes, mais d'indémontrable. Je ne considère pas l'œuvre de Gödel comme paradoxale dans la nature du Crétois qui disait que tous les Crétois mentent toujours. Ou comme le paradoxe de Russell sur l'ensemble de tous les ensembles qui ne se contiennent pas. Gödel a utilisé les idées derrière ces paradoxes pour obtenir ses résultats. Pourtant, il y a une nette distinction entre ces paradoxes – qui sont donc des contradictions – et les idées de Gödel sur certaines propositions. Ces derniers sont improuvables.'
Il en va de même pour une idée de Georg Cantor, le fondateur allemand de la théorie moderne des ensembles. Il a prouvé que le nombre d'éléments de l'ensemble de tous les sous-ensembles d'un ensemble est supérieur au nombre d'éléments de l'ensemble donné.
Le nombre d'éléments de tous les sous-ensembles de tout est également un « nombre ». Mais est-ce plus grand que le « nombre » de tout ? Si vous y réfléchissez, vous tombez rapidement dans une contradiction.”
La théorie de Gödel a environ un siècle. Pourtant, de nombreux livres sur l'histoire des mathématiques s'arrêtent là. À votre avis, qu'est-ce qui a suivi ?
"Je dirais mon travail. Mais cela semble impudique, n'est-ce pas. Le fait est, comme je l'ai dit, qu'à l'époque de Gödel, l'impact de sa découverte n'était pas clair. Aujourd'hui, nous savons mieux jusqu'où s'étend sa découverte. Elle ne flotte pas quelque part dans les mathématiques supérieures, mais a des conséquences jusqu'au niveau des mathématiques qu'un élève attentif de la troisième année du secondaire peut saisir. Ou même jusqu'au niveau secondaire inférieur.'
En Flandre, la théorie des ensembles a été abolie dans l'enseignement en 1997. La politique a renié à contrecœur 22 ans plus tard. Qu'en pensez-vous ?
« Pour les élèves doués, cet enseignement peut être très intéressant, mais ce n'est pas forcément une connaissance de base. Il y a certainement plus à faire pour les étudiants instruits. Je suis associé aux États-Unis au Arnold Ross's Program, qui organise des cours d'été de mathématiques. Les participants reçoivent même des exercices basés sur certains de mes travaux récents et se familiarisent avec. Il est donc tout à fait possible d'y mettre concrètement les jeunes en contact.'
'En étendant nos méthodes, nous avons découvert des principes mathématiques supérieurs. Ça me fait plaisir'
« Je pense aussi qu'un cours de logique mathématique est indispensable. Il est incompréhensible que même certaines universités n'incluent pas une telle chose dans le programme de base pour les étudiants en licence.'
Comment évaluez-vous le niveau en mathématiques dans cette région ?
« Vous avez suffisamment de mathématiciens de haut niveau qui ont fait un travail important. (rires :) Ce n'est pas pour rien que j'ai décidé de rejoindre le groupe de recherche à Gand."
Vous croiserez peut-être Jean Paul Van Bendegem, un philosophe assez connu associé à la Vrije Universiteit Brussel.
Est-il partisan de la théorie de l'ultra-fini, et donc ne reconnaît-il pas les ensembles infinis (nier leur existence est une autre façon d'éviter les paradoxes et l'indémontrable, ndlr) † Ou est-il un intuitionniste, qui refuse ainsi les preuves hors du commun (méthode de preuve qui dit que le contraire de quelque chose ne peut pas être vrai, donc l'énoncé doit être vrai, ndlr) † En tout cas, des discussions intéressantes m'attendent."
Quel est selon vous votre meilleur résultat de recherche ?
« Il y a beaucoup de bons résultats et de preuves ! Si je devais en choisir une, qui est la preuve que la propriété de disjonction a l'existence numérique la propriété implique. Cette preuve est apparue dans la revue Proceedings of the National Academy of Sciences , sur la recommandation de Kurt Gödel lui-même, trois ans avant sa mort.'
Lequel de vos résultats a eu le plus grand impact ?
« Mon travail en mathématiques inversées a eu pas mal de conséquences. Dans ce domaine de la logique mathématique, les scientifiques tentent de déterminer quels axiomes sont nécessaires pour prouver certains théorèmes. On procède donc en sens inverse et on voit quelles propositions on souhaite pouvoir proposer, et quel est le nombre minimum de règles de base pour cela.'
"Mais j'aime aussi la théorie sur les arbres binaires et les graphes sur laquelle vous-même, Andreas, faites également beaucoup de recherches avec les personnes de votre groupe (un arbre binaire est un diagramme simple, comme un arbre généalogique ou une série choix oui-non, mais dans lesquels des difficultés mathématiques surgissent rapidement, ndlr) .'
Vous êtes depuis longtemps un fan d'échecs. Pouvez-vous présenter un problème ?
"Je pourrais en donner des dizaines ! Je travaille même sur une théorie mathématique des échecs et un livre avec des problèmes d'échecs de nature mathématique, mais en fait je ne veux pas les partager pour l'instant. Désolé .'
Vous avez également une passion pour la musique pour piano, en particulier celle de Vladimir Horowitz, un virtuose du clavier américain d'origine ukrainienne, connu pour son jeu très contrasté.
"Je pense qu'Horowitz a joué du piano au niveau le plus créatif, et que la créativité est l'essence même de son jeu. Je sais que j'ai une approche plutôt inhabituelle des mathématiques et de la musique pour piano, et j'ai l'intention d'approfondir cela dans les années à venir. Vous vous demandez peut-être s'il existe un lien entre les deux. Bien sûr qu'il y en a! Et j'espère démontrer à l'avenir que ce lien peut effectivement être prouvé.'
Considérez les «arbres finis», qui sont des ensembles finis de nœuds reliés par des lignes, où pour un nœud donné, il y a exactement une façon d'aller de ce nœud au nœud inférieur. Il n'y a donc pas de branches qui grandissent et se refondent les unes dans les autres. Un arbre est dit « intégrable » dans un deuxième arbre s'il existe une règle qui mappe les nœuds du premier arbre aux nœuds du deuxième arbre et qui préserve la structure arborescente du premier arbre. Une rangée d'arbres, B1 , B2 , ..., BM est dit 'non-K-chaotique' si pour un nombre donné K le nombre de nœuds du i-ème arbre est au plus K+i. Par exemple, si l'on prend K=3, alors le nombre de nœuds du premier arbre peut être au plus 4, du deuxième au plus 5, du troisième au plus 6, et ainsi de suite. Une déclaration (en arithmétique) indémontrable de Friedman se lit maintenant :pour un nombre donné K, il existe un nombre M suffisamment grand pour qu'une ligne arbitraire non K-chaotique d'arbres B1 , B2 , ..., BM , permet toujours de prendre deux nombres m et n inférieurs ou égaux à M où m est inférieur à n et le mème arbre peut être plongé dans le nème arbre.
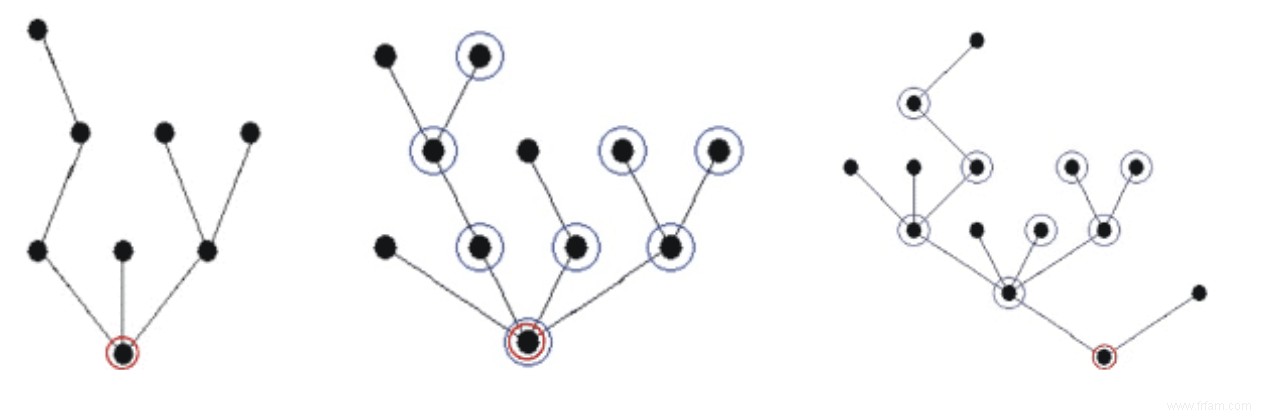
L'arbre de gauche peut être "intégré" au milieu et dans l'arbre de droite, comme indiqué par les cercles bleus. Les cercles rouges indiquent les racines des arbres.

Dans cet exemple, pour K=3, le nombre de nœuds du i-ème arbre ne dépasse pas 3+1 et la rangée d'arbres n'est donc pas 3-chaotique. Mais pour M=10 il n'y a pas de nombres m et n inférieurs ou égaux à M avec m
Harvey Friedman (°1948) est un mathématicien américain de l'Ohio State University aux États-Unis. Il est spécialisé dans la logique mathématique. En 1974, il a été conférencier au Congrès international quadriennal des mathématiciens, le plus important congrès de mathématiques au monde. Dix ans plus tard, il remporte le prestigieux prix Alan T. Waterman. En 2007, le prix des conférences Tarski a suivi. À propos de son travail, le livre Harvey Friedman's Research on the Foundations of Mathematics a été publié en 1985. .