Le berceau des mathématiques est-il en Afrique centrale ? Un os vieux de 22 000 ans avec des incisions, déterré à Ishango, au Congo, le suggère. Le découvreur, Jean de Heinzelin, a eu une autre surprise sur son lit de mort :un deuxième os d'Ishango. Il est resté dans son tiroir pendant un demi-siècle. La gemme est cruciale pour confirmer ou infirmer les différentes hypothèses sur la première barre de comptage.
Cet article est issu de nos archives et est remis à jour suite à la demande de l'Institut National pour la Conservation de la Nature (ICCN) du Congo à la Belgique de restituer les ossements d'Ishango.
Une seule jambe pourrait céder sous le poids des hypothèses qui s'y accumulent », est devenue une expression récurrente dans les discussions sur l'os congolais d'Ishango, le plus ancien témoignage indiscutable de la logique et du début du comptage. Une deuxième étape Ishango doit régler la question.
Le mathématicien anglo-indien George Gheverghese Joseph a utilisé pour la première fois l'image des hypothèses lourdes dans son ouvrage désormais renommé The Crest of the Peacock (1991), sur l'histoire des mathématiques extra-européennes. Lorsqu'il a suggéré la section sur l'Afrique, Joseph a noté que les données n'étaient pas très abondantes, contrairement, par exemple, aux mathématiques arabes, indiennes ou chinoises. L'os d'Ishango avec ses encoches ordonnées était un exemple plutôt isolé. Le géologue-archéologue belge Jean de Heinzelin de Braucourt a trouvé l'os à la frontière entre le Congo et l'Ouganda, sur les rives du lac Rutanzige (anciennement lac Edouard) et de la rivière Semliki. À l'époque, les conclusions bouffies sur les origines africaines des mathématiques semblaient farfelues, et comme le journal critique The Skeptical Inquirer prouvé, un agenda politique afro-américain dominait parfois le monde scientifique.
Mais, entre-temps, des recherches scientifiques récentes ont complètement complété les données. La tige s'est avérée avoir 22 000 ans, et non 8 500 ou 11 000 ans comme on le supposait auparavant. Et ce n'est pas sans importance :les trésoreries de certains musées se sont avérées avoir des bâtons de comptage similaires.
La cerise sur le gâteau était un deuxième os d'Ishango, qui traînait dans un tiroir depuis une cinquantaine d'années. Les différentes hypothèses sur la signification du premier bâton Ishango pourraient ainsi être confirmées ou infirmées. Curieusement, ce n'est qu'à la fin de sa vie, en 1998, que De Heinzelin a rassemblé ses notes et rédigé un brouillon pour une publication. Aujourd'hui, à l'occasion du cinquantième anniversaire du premier bilan des fouilles d'Ishango, le 28 février 2007, l'Institut royal des Sciences naturelles de Belgique (IRSNB) à Bruxelles et le Musée royal de l'Afrique centrale (MRAC) à Tervuren reprennent le défi, et publier à titre posthume le second Ishangobeen.

La Heinzelin elle-même avait porté l'os d'Ishango à l'attention du grand public avec une publication dans Scientific American (1962) et Claudia Zaslavsky (1917-2006) ont fait connaître le sujet aux mathématiciens, afro-américains et africains dans son livre Africa Counts ( 1973). Leurs récits ont été répétés plusieurs fois depuis.
Le premier os d'Ishango est un objet curieux en soi :un petit ustensile mesurant seulement quatre centimètres, avec un cristal de quartz bien fixé à une extrémité. On dirait qu'il s'agissait d'une sorte d'outil d'écriture ou de gravure, ou même d'un crayon préhistorique. Quoi qu'il en soit, les caractéristiques les plus intrigantes restent les trois colonnes d'encoches ou d'éperons disséminés le long de l'axe longitudinal. L'une est du côté courbe et a été appelée la colonne M par De Heinzelin (Environnement), les autres sont désignées G (Gauche) et D (Droite). Dans chaque colonne, les encoches à peu près parallèles sont disposées en groupes bien visibles, bien qu'elles diffèrent en longueur et aient des orientations légèrement différentes :
Colonne G :11 13 17 19
Colonne M :3 6 4 8
10 (=9+1) 5 5 7
Colonne D :11 21 19 9
Les marques de la jambe ont intrigué De Heinzelin. Il a contacté, entre autres, Lancelot Hogben, un mathématicien apprécié à l'époque de De Heinzelin. Il venait de terminer le livre Mathematics for the Million écrit. Nous citons brièvement :« La base 2 apparaît sur la jambe par le principe du dédoublement [M-colonne] et le tableau de 4; la base 10 par sa position centrale et la répétition des opérations faisant référence à 10 et ses multiples, la séparation des M<_10, G et D<_9, et des nombres 10±1 et 20±1 [D colonne ]. De plus, le choix des nombres premiers [colonne G] suggère que la connaissance des opérations supérieures telles que la multiplication et la division était connue. En bref, cela aurait été une "table magique" montrant des connaissances arithmétiques avancées :(a) addition, soustraction, doublement et multiplication (hors division), (b) bases 2 et 10, 10 étant vu sous la forme '9+ 1', (c) nombres premiers, (d) le plus grand nombre rapporté est 21, (e) le plus grand nombre obtenu par opérations est 60.'

L'ami de Heinzelin, le professeur Libois, a approuvé l'interprétation du jeu arithmétique :‘ L'homme le plus ancien a perçu les propriétés des nombres en manipulant de petits tas de cailloux, d'os, de haricots, de grains ou de grains." Des preuves proches des récits ethnologiques confirmeront plus tard ces hypothèses intuitives, ainsi que le mélange supposé de l'utilisation de différentes bases. En outre, des doublements et des réductions de moitié ont été observés à travers l'Afrique dans la méthode de multiplication dite «rurale», ou encore, dans la «méthode d'adaptation» du Sénégal. L'hypothèse plus récente de Heinzelin selon laquelle 3, 5, 7, 11, 13, 17, 19 représentent une liste de nombres premiers (bien que l'ordre sur la tige soit différent) est plus discutable, tout comme une autre proposition plus récente selon laquelle la tige représente également la connaissance de 'zéro'. Nulle part en Afrique sub-saharienne l'utilisation des nombres premiers ou du zéro n'a été établie.
Ce manque de preuves substantielles contraste avec l'interprétation suggérée par Alexander Marshack. Les colonnes G et D donnent un total de 60 =5x12, et la colonne M 48 =4x12, ce qui correspond à deux mois lunaires et un mois lunaire et demi. Marshack a examiné l'os au microscope, en tenant compte non seulement du nombre d'encoches, mais également de leur différence de taille et de forme, ainsi que de l'ordre des sous-groupes. Les lignes plus petites et plus épaisses indiqueraient les différentes phases de la lune, selon une sorte de rythme ou de motif. Marshack avait commencé sa carrière comme journaliste passionné et devint plus tard archéologue. Il a commencé et conclu son volumineux ouvrage Roots of Civilization avec l'hypothèse que la jambe d'Ishango était un calendrier lunaire.
Pourtant, l'interprétation de Marshack est difficile à saisir. Son étude similaire de la plaque osseuse de Blanchard, de Dordogne, France, n'a pas été acceptée à l'unanimité. De plus, la tige est clairement trop petite pour être réellement utilisée comme calendrier. Il est vrai que les civilisations africaines fabriquaient des calendriers avec des pattes et des cordes. Le rôle de la lune dans de nombreuses coutumes a été élucidé dans la littérature. Certains y voient même un lien avec des versets de l'Iliade d'Homère , lorsque l'écrivain grec déclare que "oi Pygmaioi" vivait près des rives du Nil et "apparaissait à l'apparition saisonnière des grues, dans des batailles sanglantes pour défendre les récoltes dont elles subsistaient". À Ishango, cependant, le microclimat local n'a pratiquement pas de saisons et les gens vivaient dans une communauté prospère, sans risque d'épreuves récurrentes.
Une catastrophe a cependant profondément bouleversé la communauté d'Ishango :une éruption majeure dans la zone volcanique de Katwe, à quelques kilomètres à l'est. Elle a étendu une couche de cendres et de tuf de plusieurs mètres d'épaisseur sur une surface considérable.
L'éruption volcanique a fourni un avantage pour la reconstruction de l'histoire de l'Ishangosite :il s'agit d'une séquence bien conservée de couches superposées de matériel lithique et osseux. Il n'y avait aucune trace de structures d'habitation, car les strates n'étaient constituées que d'ajouts successifs de «déchets» d'habitations riveraines, tels que des artisanats de petits cristaux de quartz, des meules, des rouleaux grappins, des flèches, des crochets et une grande quantité d'os polis. De Heinzelin pouvait distinguer avec précision l'origine des différents types de harpons à poisson. Cela montre qu'Ishango était un lieu privilégié pour une civilisation, et qu'il était habité en permanence.
L'inconvénient de l'éruption volcanique de Katwe était qu'ils remplissaient l'eau du lac de CO tellurique2 surchargé, et ce pendant longtemps. Cette abondance inerte de C12 a vieilli et modifié les rapports habituels d'isotopes dans les eaux du lac à tel point que même les coquillages modernes ont été datés de 1 000 avant JC (même longtemps après l'éruption de Katwe). Dans l'atmosphère également, le rapport C14/C12 n'était pas nécessairement constant et n'était pas égal à celui actuel, de sorte que la quantité de carbone ne peut pas être utilisée comme référence. Ainsi, De Heinzelin, géologue, s'en tient à une « chronologie stratigraphique générale », basée sur les indications d'altitude, d'environnement, de décomposition du sol et de dépôts trouvés. Cela l'a conduit à une approximation de 8 000 avant JC, c'est-à-dire la période de transition du Pléistocène à l' Holocène; il continuerait à défendre cette date.
Le désaccord avec le reste de la communauté des chercheurs archéologiques a peut-être été l'une des raisons pour lesquelles De Heinzelin n'a pas été très encouragé à poursuivre ses rapports Ishango, donnant la priorité à ses autres découvertes plus universellement acceptées. Les défenseurs du « chronométrage absolu » ont daté les obus d'Ishango grâce au radiocarbone. Ils datent maintenant les tiges d'Ishango entre 21 000 et 23 000 avant JC. De Heinzelin est sensible à leurs arguments et pointe même leur travail :« On ne peut ignorer les fouilles de John Yellen, qui ont eu lieu en 1988-1989 à Katanda, à trois kilomètres en aval sur la rive droite de la Semliki. Une industrie caractérisée par des harpons plus épais que ceux d'Ishango était associée à des éléments paléolithiques. Elle est clairement plus âgée […]'. En effet, un âge de 90 000 ans s'est avéré correct pour ces autres sites similaires à Ishango. Dans ce contexte, l'affirmation selon laquelle la culture qui a fabriqué les tiges d'Ishango avait environ 22 000 ans semble encore plutôt conservatrice.
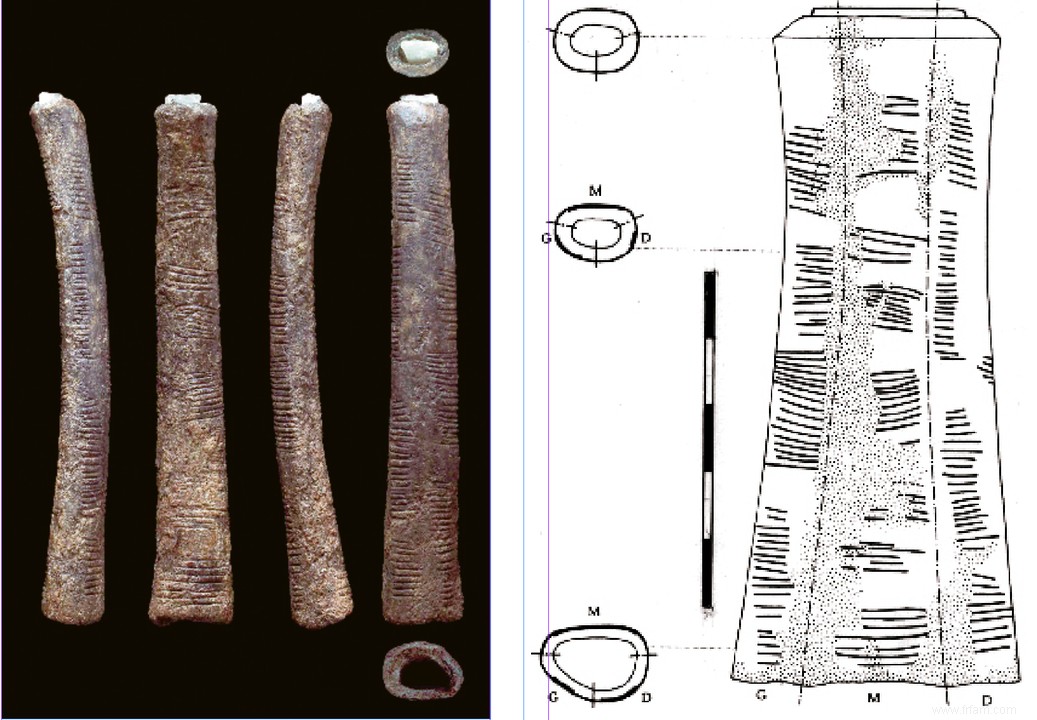
Gauche :La première étape d'Ishango sous six angles différents. A droite :Le dessin Heinzelins, de 1957, sur lequel les sillons sont bien visibles.
L'attribution de la découverte des concepts arithmétiques à un petit groupe de néolithiques au cœur de l'Afrique est, selon une critique plus générale, très surprenante. La communauté aurait été coupée d'autres colonies importantes. Cependant, cet isolement relatif ne semble pas correspondre à ce que les historiens ont appris sur les zones de la région. Des voies d'échanges culturels ou commerciaux existaient au sud et à l'est du Sahara, et la route d'Ishango via Khartoum à l'Egypte en longeant le Nil, et de Khartoum à l'Afrique de l'Ouest était également acceptée par certains historiens, bien que des doutes s'élèvent progressivement quant à sa signification. cet itinéraire. Les contacts entre les populations n'impliquaient pas nécessairement un échange culturel, et les liens évidents entre la culture primitive Ishango et les Bushmen éclairent différemment la direction géographique de tout échange.
Même l'une des caractéristiques les plus attrayantes d'Ishango, son emplacement aux sources actuelles du Nil (avec le lac Victoria et le plus petit lac de la Lune), a perdu son importance. La « terrasse » où ont eu lieu les fouilles est à une dizaine de mètres de haut au-dessus du lit actuel de la rivière Semliki, mais il y a plusieurs milliers d'années, la rivière a drainé les coulées de glace du Ruwenzori. Le site archéologique d'Ishango est donc un delta fluvial d'un lac de glace sur les flancs des monts Ruwenzori. La formation du delta a pris beaucoup de temps et montre qu'il y avait une habitation côtière permanente de pêcheurs, chasseurs et cueilleurs. Ce n'est que récemment que des changements géographiques ont fait couler l'eau de la Semliki vers le Nil.
Malgré tout cela, on ne peut exclure qu'il existait dans l'Antiquité une voie privilégiée le long du Nil pour l'exportation de produits exotiques des grands lacs d'Afrique centrale vers les rives de la Méditerranée. Pourtant la diffusion de la civilisation Ishango vers le Nord, juste avant l'ère pharaonique de l'Égypte, était déjà démontrée par la comparaison des harpons courts trouvés à Khartoum et dans la région de Turkana.
A l'époque du livre de Joseph, La crête du paon , et la critique ultérieure de l'importance d'Ishango, il était en effet vrai que la plupart des artefacts tels que l'os d'Ishango avaient été trouvés en Europe, de la péninsule ibérique aux steppes russes. Marshacks Racines de la civilisation contenait pour la plupart des découvertes archéologiques d'Europe, mais c'est parce que moins de fouilles ont été effectuées en Afrique à l'époque. Ni aujourd'hui. Inspirés par les délais de 75 000 à 90 000 ans pour les harpons dentelés assez modernes trouvés près de la rivière Semliki, les manuels actuels indiquent que les humains modernes avaient des ustensiles ingénieux avant de se propager de l'Afrique vers d'autres continents. En Europe, de tels objets ont été inventés pour la première fois il y a 40 000 ans.
Les aspirations mathématiques de l'homme primitif peuvent également être déterminées à la lumière de leur probabilité, puisque les encoches logiques groupées sur les tiges d'Ishango semblent être précédées de systèmes de comptage plus simples ou de dessins encochés. Par exemple, dans les grottes des montagnes Lebombo en Afrique du Sud, un os de singe fossile a été découvert en 1987, vieux de 35 000 ans et comportant 29 gravures. Une autre pierre d'environ 70 000 ans, décrite en 2001, a des lignes presque parallèles et prouve la capacité des premiers hommes à faire des dessins presque géométriques. Les bâtons d'Ishango ont heureusement été préservés, tandis que d'autres, bâtons de bois et cordes à compter, n'ont pas résisté à l'épreuve du temps. Jusqu'au XXe siècle, les éléments d'enregistrement des quantités sont restés répandus. Les découvreurs et les missionnaires accordaient rarement de l'importance à ces bâtons de pointage ou à ces cordes à nœuds sans intérêt. Pourtant, ils ont parfois été remarqués, comme dans l'expédition de Grant et Speke, où les porteurs utilisaient de la ficelle. Exceptionnellement, des missionnaires ou des administrateurs coloniaux ont fait don de quelques objets de comptage à un musée. Le Musée royal de l'Afrique centrale de Tervuren y occupe une place particulière, car le clergé catholique – en raison de son attention particulière à l'éducation – a même inclus des rapports sur l'utilisation des bâtons sculptés ou des cordes nouées. Ils peuvent encore être consultés à la bibliothèque du MRAC. En général, ces descriptions racontent des histoires sur le comptage des jours, des semaines, des mois ou des années, et pourquoi certains événements spéciaux devaient être rappelés (comme l'accession d'un nouveau roi au trône). D'autres communiquent l'enregistrement des paiements, des prêts, de la distribution d'eau, des marchandises à transporter, des dents en ivoire vendues, etc.
Sture Lagercrantz a consacré trois longs articles de synthèse aux cordons de comptage africains, aux bâtons de comptage et aux coupures ou tatouages sur le corps. « Compter à l'aide de pierres, de noix, de bâtons, de feuilles d'herbe et d'objets similaires est une pratique ancienne qui a été particulièrement remarquée au Soudan du Sud. La méthode de comptage peut être comparée à celle du comptage des cordes. Ces derniers étaient plus dispersés au nord, mais ils appartenaient à la même culture noire. Les éléments culturels anciens comprennent également le comptage avec des lignes tracées au sol, sur les portes et les murs. »
Zaslavsky a décrit comment les Peuls du Niger dans le nord du Nigeria plantaient deux courts bâtons dans le sol en forme de V, pour indiquer qu'ils avaient 100 animaux, tandis qu'une croix, un X, en indiquait 50. Les bâtons horizontaux sont notés 10, les verticaux les unités, donc =||| 23, tandis que VVVVVVX|| représentait 652. Ces derniers temps, ces affirmations ont été largement étayées. dr. Mubumbila Mfika, un chimiste gabonais, a reproduit les schémas des Bashongo de l'est du Congo, qui traçaient des lignes dans le sable avec trois doigts d'une main, et complétaient trois groupes de trois avec une seule ligne :||| † † † Les Bambala comptaient par cinq, mais les Bangongo, Bohindu et Sungu par quatre. Les gestes de comptage et leurs systèmes de notation créatifs expliquent en partie les différences dans les bases utilisées en Afrique. Des témoignages récents montrent que les bases 10 ou 12 n'étaient certainement pas les seules :les linguistes découvrent encore l'usage de bases telles que 2, 5, 6, 12, 16, 20, voire 32. Par exemple, certains peuples ne disent pas 17 comme '7 et 10', mais comme '3 sur 20' ou comme '5 et 12', ou utilisez pour 37 des expressions telles que '3 moins que 2-20' ou '32 plus 5'. Les habitudes de comptage font appel à l'imagination et remontent aux temps les plus anciens, comme le souligne Lagercrantz (avec une allusion involontaire à Ishango) :« L'ancienne coutume de compter le nombre d'ennemis tués en taillant la propre peau du guerrier était très répandue. dans la zone autour du lac Albert (lac Rutanzige), et de l'autre côté dans la zone centrale de l'Afrique du Sud. Cela confirme les liens ethnographiques bien documentés entre l'Afrique du Nord-Est et l'Afrique australe. »

Bâtons sculptés du siècle provenant des trésoreries du MRAC de Tervuren (catalogue :EO.0.0.1816 ; EO.0.0.34992 ; EO.0.0.2144 ; toutes les photos :ADIA, IRSNB Bruxelles ; tous les objets :collection du MRAC (c )).
Des découvertes récentes suggèrent une troisième interprétation de la tige Ishango. Le "jeu arithmétique" de Heinzelin avec des nombres premiers, sans mentionner d'autres faits arithmétiques tels que des carrés ou des cubes, ferait une curieuse transition du comptage élémentaire à un concept abstrait. L'interprétation de Marshack en tant que calendrier lunaire n'est pas confirmée dans les calendriers africains traditionnels sur les nœuds et les bâtons, qui énuméraient simplement les jours, bien que sur une plus longue période de temps. Pourtant, la logique indéniable sur la jambe appelle une explication, mais peut-être n'avons-nous pas besoin de chercher plus loin que cela est un témoignage ordinaire d'une méthode de comptage qui mélangeait les bases 6 et 10. Un tel processus de comptage est même courant selon les normes occidentales :par exemple, lorsque le résultat d'une élection doit être compté sur une feuille de papier ou un tableau, les nombres sont souvent groupés par 5, puis en deux groupes de cinq, car la base 10 est généralement à l'ouest :|||| † † † † † … Les quantités de petits objets, comme les sous ou les jetons, en revanche, sont souvent comptées par paires :2, 4, 6, 8, 10, … De plus, des bandes de longueurs différentes sont souvent appliquées sur une latte :|
Par exemple, si la communauté Ishango avait prononcé son mot pour 7 comme 'un-trois-trois', il serait probable que les scribes le 'traduiraient' comme | |||||| , et ce fut le cas sur la tige. Les encoches pour 10, dans la rangée M du milieu, montrent 9 + 1, ce qui rappelle involontairement le mot swahili contemporain pour le nombre neuf, à savoir "kenda", qui signifie "en emporter un". La seule opération arithmétique évidente sur la tige d'Ishango, le doublement, peut être interprétée de la même manière, puisque 8 est compris dans de nombreuses langues africaines ou dans les dessins de sable comme 'ne-na-ne', et c'est 'quatre- et-un'.-quatre'. Bien sûr, cela aurait pu à son tour conduire à la méthode de multiplication telle qu'établie en Égypte, en Afrique de l'Ouest ou en Éthiopie.
Si ce n'était pas le mélange d'une base 10 et 2 mais d'une base 6 et 10 qui était d'usage chez Ishango, cela expliquerait pourquoi les sommes des colonnes sont 60 et 48. De manière analogue, si les bases 10 et 2 étaient mélangées, davantage de groupes de 100, ou 20 et 40, auraient émergé. Il se pourrait donc bien, par analogie avec la colonne D qui montre un schéma clair de 10±1 et 20±1, que la colonne G puisse être lue comme 12±1 et 18±1, éventuellement précédés de la fin de la colonne M, où 5 et 7 peuvent représenter 6±1.
Les preuves de ce mélange de bases sont abondantes. Les chiffres Nyali combinent 4 et 6, alors qu'en 1920 N. Thomas observe les bases 6 sur des mots de 7 à 9 en Guinée. Le Bulanda exprimait 10 comme 6+4, le Bola 12 comme 6x2 et 24 comme 6x4. Il est curieux de noter que l'article de Thomas date de 1920, bien avant la découverte des cannes Ishango. Il suggère une connexion "naturelle" entre les mots numériques duodécimaux dans certaines régions du Nigeria et la région de Semliki. A son époque, bien sûr, il ne pouvait que penser que les concepts arithmétiques étaient transportés de l'Egypte le long du Nil jusqu'à ces régions de l'Afrique noire.
Pletser, physicien et ingénieur, a fait une suggestion très audacieuse selon laquelle il pourrait y avoir un lien entre les différentes colonnes, comme la possibilité que le 13 sur la colonne G puisse être la somme du 3-6-4 dans la colonne du milieu. . Cela rappelle les anciennes règles à calcul utilisées par les ingénieurs lorsqu'il n'y avait pas de calculatrice, mais cela pourrait aussi être une simple conséquence de la disposition des rangées d'encoches en colonnes. Lorsque, par exemple sur une planche, deux rangées d'encoches |||| † ...sont écrits les uns en dessous des autres, ils sont souvent disposés de manière à ce que le premier caractère de chaque ligne soit disposé exactement en dessous de l'autre, le long d'une même ligne verticale invisible. Cette relation entre une représentation graphique et la technique de comptage correspondante peut à son tour avoir eu des conséquences indirectes pour l'arithmétique, comme l'a souligné Pletser. Dans l'ensemble, cette interprétation plus équilibrée rend la jambe d'Ishango moins spectaculaire, car elle n'implique pas de nombres premiers ou d'astronomie, et ne fait pas appel à «l'excès» mathématique. C'était peut-être une bonne chose, mais le test ultime était encore à venir.
Les fouilles à Ishango se sont déroulées entre 1950 et 1959 en plusieurs phases. Dans ce dernier, Marcel Spinglaer, le chef technicien qui travaillait dans le département de De Heinzelin, a apporté une autre jambe crantée. Cela explique pourquoi le rapport détaillé de 1957 a omis de mentionner son existence et pourquoi sa publication en 1962 dans Scientific American , qui était un résumé, était muette à ce sujet. Il a fallu des années pour obtenir les informations sur le match retour, et la confirmation de l'interprétation de Pleter a dû attendre tout ce temps, ce qui a naturellement augmenté la tension.
Le match retour s'est retrouvé dans un niveau proche du premier, sans aucune différence de timing. Pour rappel, les couches excavées ont été formées par des ordures ménagères et non par des fondations de maisons, il reste donc incertain si les deux 'bone-kickers' se connaissaient ou non. Cependant, il est très probable qu'ils aient vécu dans un environnement similaire et aient eu une éducation similaire.
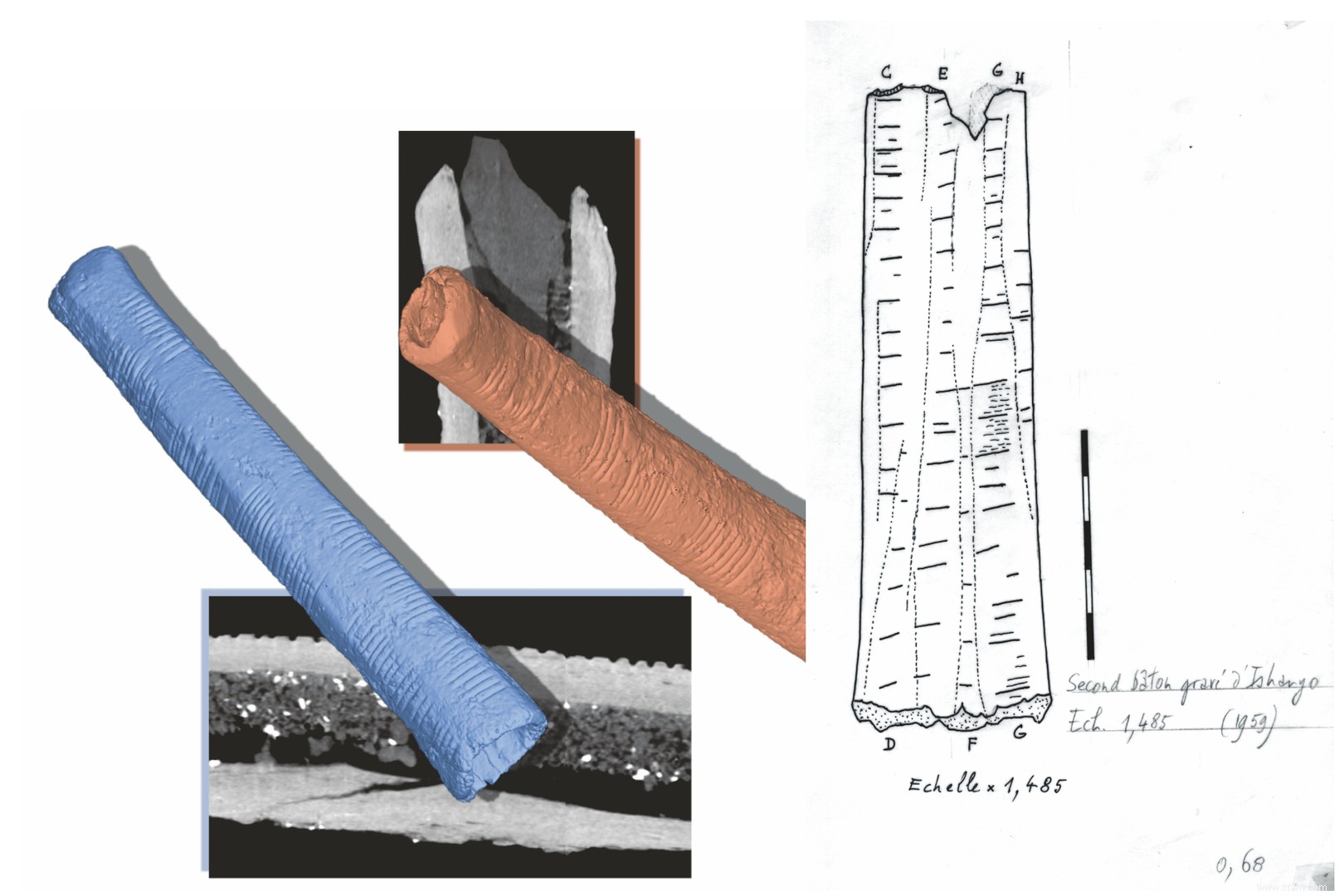
A gauche une image 3D de la première jambe, réalisée avec un scanner médical. Il montre l'intérieur et la manière dont le cristal est fixé. À droite, un dessin du deuxième os d'Ishango, pierre de touche de nombreuses hypothèses sur le premier décompte mathématique.
La jambe est un peu plus longue, et a une section creuse au milieu, un arbre d'une longue jambe, dont la détermination anatomique est discutable à ce jour. La jambe semble avoir été redressée par grattage et lissage et est bien conservée, quoique cassée à une extrémité. Peut-être qu'un cristal de quartz y était attaché, comme ce fut le cas pour la première jambe, confirmant ainsi que la culture Ishango utilisait des objets pour la sculpture, l'écriture, ou même à des fins didactiques.
Le match retour comporte 6 rangées, que De Heinzelin a numérotées C, D, E, F, G et H :
C :14 encoches longues; 6 courts.
D :6 encoches longues.
E :17 encoches longues; 1 court.
F :6 de long.
G : 20 de long.
H :6 encoches longues; 2 courts.
De Heinzelin a ajouté que la petite encoche sur la colonne E est à la "place de 10" et s'est demandé si cela "marquait une transition de la base 10 à 12". Voici une description plus détaillée de la colonne G plus problématique :
Court 4' ; court 6'; deux encoches jumelles courtes entre 7 et 8 ; une courte encoche 9' après 9 ; portion de tapis entre 10 et 12 (deux bases numériques ?); deux encoches courtes 18' et 18'' entre 18 et 19 (ou des tiers ?); quatre crans courts entre 19 et 20 (ou quintes ?); court 20'.
Étant donné que la rangée C a un total de 20 traits et la rangée E 18 (les traits courts ici sont assez longs), les bases 6 et 10-20 semblent avoir été utilisées. De plus, il existe deux similitudes spatiales entre les lignes, à E10 =F1 =G10 et à E12 =F2 =G12.
Il est clair qu'il n'y a pas de nombres premiers maintenant, ni qu'un calendrier de mois lunaires peut être distingué. Dans les jours précédant sa mort, De Heinzelin lui-même semble avoir adopté les hypothèses de Pletser sur un mélange de bases 6 et 10 et la règle de calcul, bien qu'il n'ait jamais connu Pletser :« Cela nous rappelle un peu l'équivalence entre les deux bases 10 et 10 12 (décimal et duodécimal). Il faut associer la répétition des 6 unités des rangs raccourcis aux parties sourdes de Sol entre 10 et 12. L'accentuation avec les petites encoches justifie l'idée d'une règle mathématique.'
Les cristaux de quartz sur les os d'Ishango rendent la découverte plus intrigante que les chiffres des trésors des musées africains d'aujourd'hui et les descriptions des missionnaires et des administrateurs. Parce que les Ishango ont conçu leurs nombres dans une combinaison de base de 6 à 10, comme les peuples de tant de régions africaines aujourd'hui, une logique indubitable émerge, que ce soit exprès ou non. C'est ce que suggérait en 1999 l'auteur de cet article, à partir d'équations ethnologiques sur la première barre, sans connaître la seconde. Bien sûr, l'importance de la découverte reste à démontrer :le mélange des Ishangobases 6-10 a-t-il bien atteint l'Egypte ? En d'autres termes, le peuple Ishango a-t-il été poussé vers le sud jusqu'au Botswana actuel ? Nous ne pouvons qu'espérer que les archéologues feront plus de fouilles en Afrique, ou que les ethnologues regarderont également leurs collections à travers une lentille mathématique, pour le bien des sciences exactes, et surtout pour le bien de l'Afrique elle-même.
Dirk Huylebrouck, Département d'architecture Sint-Lucas (Bruxelles) remercie Ivan Jadin et Patrick Semal, Institut royal des Sciences naturelles de Belgique (Bruxelles) et Els Cornelissen, Musée royal de l'Afrique centrale (Tervuren), ainsi que Vladimir Pletser de le Centre européen de recherche et de technologie spatiales (ESTEC, ESA) (Noordwijk). L'aide du MRAC et du groupe ADIA de l'IRSNB pour trouver les illustrations appropriées a également été très appréciée.