À l'occasion de la Journée nationale de la poésie, les blogueurs mathématiques écrivent sur leurs poèmes (mathématiques) préférés.
La poésie est de tous les temps, cultures et langues. La poésie appartient au peuple, pour le peuple. Et même s'il semble souvent que les mathématiciens n'ont rien à voir avec le langage, ou les linguistes rien à voir avec les mathématiques :rien ne pourrait être plus éloigné de la vérité. Tout comme nous, les mathématiciens, aimons profiter d'un bon poème de temps en temps, il existe de nombreux exemples de poètes qui ne cachent pas le fait qu'ils ont aussi un talent pour les mathématiques (ou d'autres sciences exactes). Nous sommes heureux de partager un aperçu de certains de nos écrits préférés.
La poésie est née bien avant l'écriture. Dans le passé, les histoires étaient généralement transmises oralement, et l'utilisation de formes de vers ou de rimes spécifiques facilitait la mémorisation de ces histoires. Mais ce qui peut servir à des histoires, peut aussi servir à des formules compliquées ! C'est ainsi que Niccolò a découvert Tartaglia il y a environ 500 ans une formule pour résoudre certaines équations cubiques. Son collègue mathématicien Girolamo Cardano voulait connaître cette formule aussi, et a promis de ne pas publier la formule. Tartaglia a sauté le pas et a partagé la formule dans une lettre, quoique sous forme de poème :

Ce que Tartaglia décrit en fait ici d'une manière quelque peu énigmatique, c'est que vous pouvez trouver la solution d'une équation $x^3+px+q=0$ (avec des nombres aléatoires $p$ et $q$) au moyen d'une astuce ingénieuse . En fin de compte, cela conduit à la solution plutôt compliquée $x =\sqrt[3]{\frac{-q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{ 27 }}} + \sqrt[3]{\frac{-q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$, qui Cardano a également déchiffré. Il publia néanmoins la formule sous son propre nom, provoquant une importante querelle entre les deux messieurs. (Vous pouvez en savoir plus à ce sujet dans cet article de blog précédent.) Une traduction (en anglais) du poème, y compris la signification mathématique complète, peut être trouvée dans cet article.
Dans la même catégorie de mnémoniques, il y a deux ans, le jour pi, nous avons également parlé de quelques poèmes qui ont été développés pour se souvenir des décimales du nombre pi. Mais quiconque a suivi de près nos faits pi ces dernières années (2019, 2018) sait qu'il existe également de nombreux autres poèmes pi (ou piezie ?), comme le poème « Pi » du lauréat du prix Nobel Wisława Szymborska. L'un des meilleurs exemples, cependant, est le poème "Decimalen" du virtuose de la langue et comédien suisse (mais néerlandophone) Heinz Polzer, mieux connu sous le nom de Drs. P. , plus tard également mis en musique par lui sous le nom de "tango grec":
«Decimals» est apparu dans le recueil de poèmes «Wis- en natuurlyriek» des Drs. P. et Marjolein Kool. Les deux auteurs parviennent à traiter divers sujets et personnes des mathématiques, de la physique et de la chimie dans la poésie de manière magistrale et avec une bonne dose d'humour, et si nécessaire les expliquent de manière accessible avec les connaissances nécessaires. Vous pouvez voir un échantillon limité du bundle via ce lien. De Marjolein Kool nous aimerions partager le poème "Prouve" (pour votre information :une preuve par contradiction est une méthode de preuve issue de la logique mathématique, dans laquelle on suppose qu'une certaine proposition n'est pas vraie, car cette hypothèse rencontre une contradiction, et donc conclut que l'énoncé en question doit être vrai) :
Un tyran a récemment crié avec panache
armé d'une feuille de A-5 :
'Il n'y a pas de plus grand nombre,
c'est ce que je vais prouver.
Supposons que si je devais vous tromper
et que je plaisantais ici,
alors je pourrais nommer le plus gros sans exagération
.
Mais j'ai fini, vous criez méchamment :
« Augmentez ce nombre de deux ! » />alors vous remarquerez :c'est sans limite.
Et avec ça j'ai qed
Je suis si heureux à cause de cela.
Continuez comme ça, dit-il avant de s'évanouir,
'prouver le non-poème.'
Sans surprise, encore plus de théorèmes mathématiques ont été versés dans la poésie. L'un des créatifs maîtrisant parfaitement les deux domaines était Sir Frederick Soddy. (également lauréat du prix Nobel de chimie en 1921). En 1936, il redécouvre un théorème déjà proposé par René Descartes . était connue au XVIIe siècle. Supposons que vous ayez trois cercles qui se touchent (les cercles noirs dans la figure ci-dessous), alors il y a deux possibilités pour tracer un quatrième cercle (en rouge) qui est également tangent aux trois noirs :un petit à l'intérieur et un grand autour de.
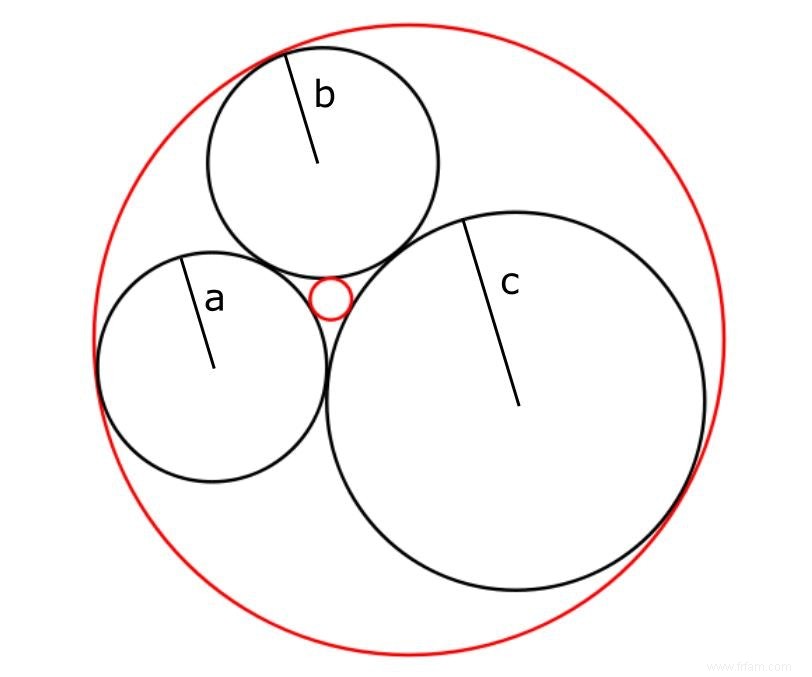
Soient $a$, $b$ et $c$ le rayon des cercles noirs, alors pour le rayon $r$ de l'un des cercles rouges, il est vrai que $\frac{1}{a^2}+\frac {1}{b^2}+\frac{1}{c^2}+\frac{1}{r^2} =\frac{1}{2}\left(\frac{1}{a} +\frac{1}{b}+\frac{1}{c}+\frac{1}{r}\right)^2$. Soddy est devenu célèbre pour cette déclaration principalement en raison de la manière dont il l'a fait connaître au monde extérieur :à travers le poème « The Kiss Precise ». Plus tard, cette déclaration a même été généralisée, le poème étant développé de manière appropriée :d'abord par Thorold Gosset (1937) qui a décrit une relation similaire dans n'importe quel nombre de dimensions, et ensuite par Fred Lunnon (2001) qui ont également considéré la géométrie elliptique et hyperbolique.
Un autre exemple est le célèbre dernier théorème de Fermat , qui stipule qu'une équation de la forme $x^n+y^n=z^n$ n'a jamais de solution où $x$, $y$ et $z$ sont des entiers positifs si $n$ est supérieur à 2. Fermat lui-même avait écrit ce théorème dans la marge d'un livre, avec les mots ailés "J'ai une preuve vraiment remarquable pour ce théorème, mais cette marge est trop petite pour l'écrire.", qui en fait aussi comme de la poésie aux oreilles. Cependant, il a fallu plus de 350 ans avant que le théorème ne soit formellement prouvé par Andrew Wiles (en deux articles qui totalisent pas moins de 129 pages...) en utilisant des courbes elliptiques, des formes modulaires et d'autres techniques mathématiques compliquées. En l'honneur de cet heureux événement, l'une des réalisations mathématiques les plus importantes du XXe siècle, un défi de poésie a été lancé, qui a abouti aux limericks suivants :
Avec un entier supérieur à 2
C'est quelque chose qu'on ne peut tout simplement pas faire.
Si cette marge était grosse,
Je vous montrerais tout ça,
Mais c'est non, alors la preuve est sur vous !
(Ted Munger)
On prend une courbe elliptique E,
Considérons les points tués par 3,
Ce "rho" doit être modulaire,
Et par des faits qui sont populaires,
La preuve de Fermat est gratuit.
(Jeremy Teitelbaum)
Que la forme poétique limerick se prête parfaitement aux mathématiques ressort également des exemples ci-dessous, qui font régulièrement le tour des réseaux sociaux, bien qu'un minimum de compétences en mathématiques soit requis pour vérifier leur brillance.
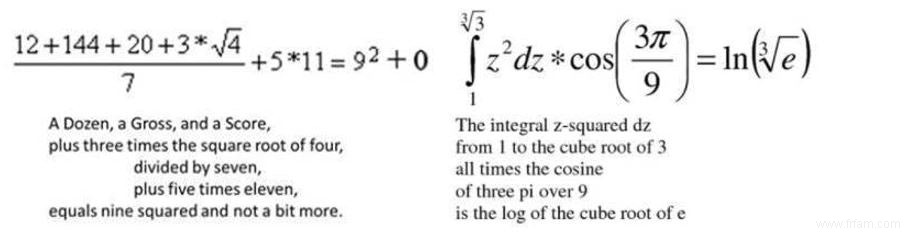
Il devrait être clair que l'amour des mathématiques est une source d'inspiration parfaite pour beaucoup de poésie. La plupart des poèmes parlent bien sûr d'amour, mais cela aussi peut être exprimé parfaitement mathématiquement. Par exemple, il y a la déclaration d'amour de The Klein Four "Finite Simple Group (or Order Two)", pleine de jeux de mots mathématiques (bien que cela ait un contenu geek relativement important, mais nous l'admettons sans hésitation). Maud Vanhauwaert (en 2018 et 2019 toujours poète de la ville d'Anvers) a écrit le poème "Nous sommes parallèles" de son recueil du même nom, avec le beau vers "elle accroche son bras au mien en une lemniscate". La lemniscate de Bernoulli est une courbe mieux connue sous le nom de symbole de l'infini $\infty$, ce qui explique immédiatement le symbolisme du poème. Ou il y a le poème visuel "Sacrifice and Bliss" de Kaz Maslanka :
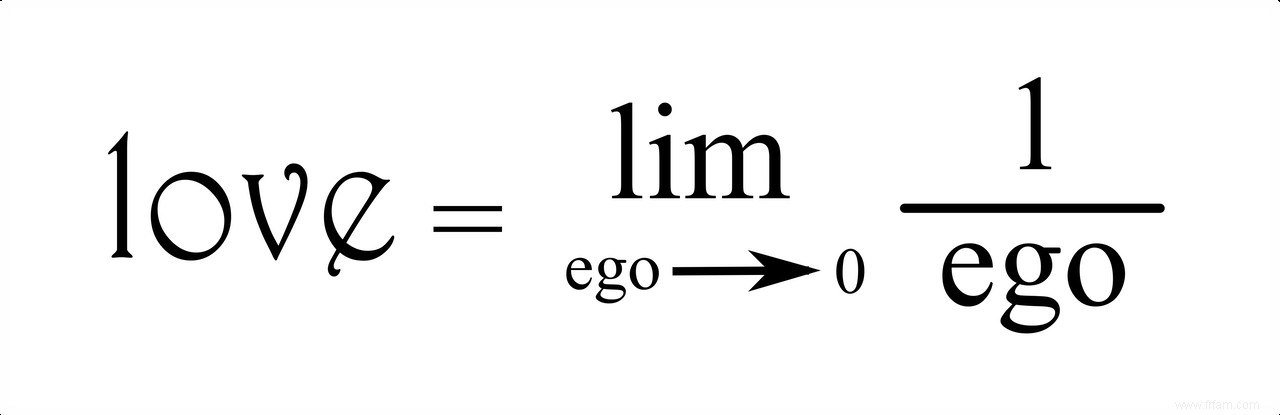
Avec un minimum de mots, Maslanka parvient à résumer l'essence de l'amour dans une formule mathématique simple :à mesure que le dénominateur de la fraction (étant l'ego) devient de plus en plus petit et se rapproche de 0, la fraction elle-même deviendra de plus en plus grande et deviendra même infiniment grand à la limite. Autrement dit :le pouvoir de l'amour est inversement proportionnel à la taille de l'ego.
Vous voulez en savoir plus ? Vous trouverez ci-dessous d'autres articles/blogs/livres sur la combinaison des mathématiques et de la poésie :
Néerlandais :
En anglais :
Français :