Walter Van Rensbergen est astrophysicien à la VUB. Non seulement il étudie les étoiles, mais il est aussi au milieu d'elles :l'astéroïde 24679 porte son nom. Dans son dernier blog, il explique le "nombre d'or" :un rapport mathématique qui est vécu comme très harmonieux dans l'architecture et l'art.
Ceci est un blog personnel de l'astrophysicien Walter Van Rensbergen de la Vrije Universiteit Brussel.
La figure (1) montre la section d'or d'un segment de droite de longueur 1. Vous le divisez en deux parties a et b. Soit a la partie longue et b la partie courte. Le nombre d'or demande que la longueur de la partie longue (a) divisée par la partie courte (b) soit la même que la longueur du segment de ligne complet (a+b) divisée par la partie longue (a). Ce rapport est le nombre d'or φ (phi):

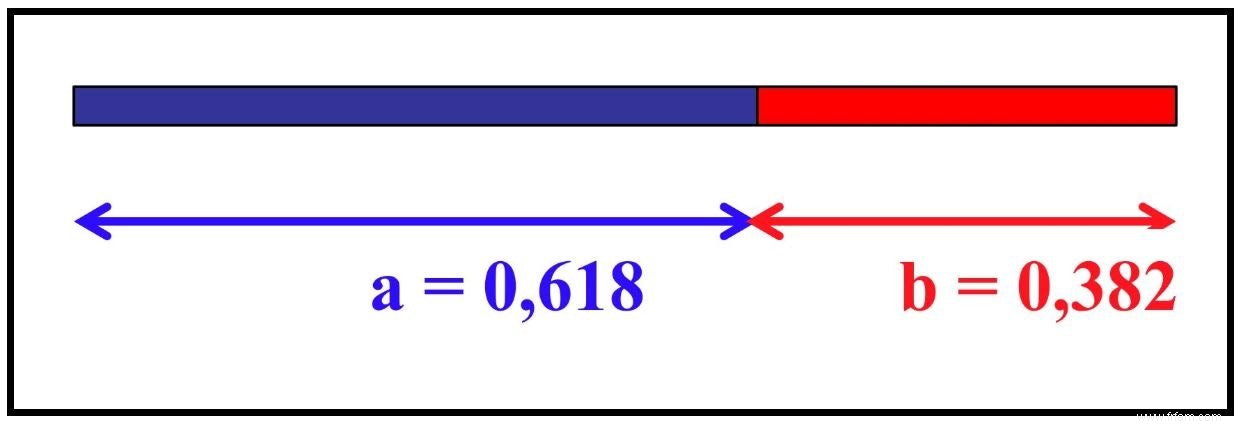

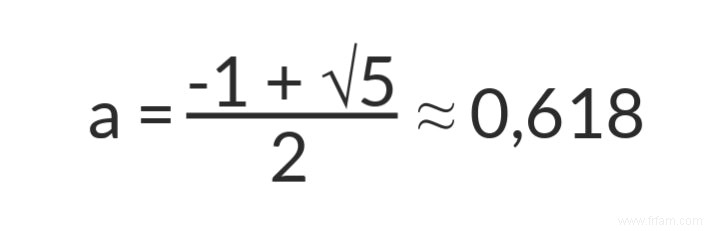
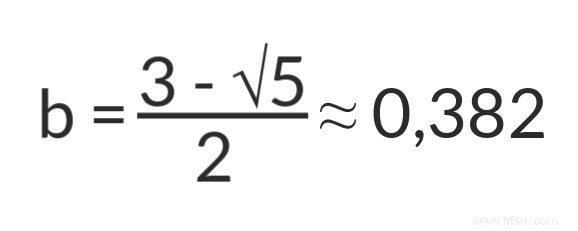
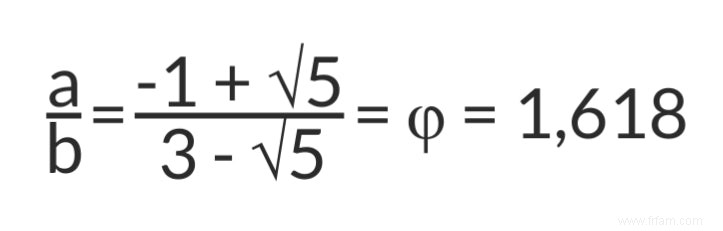
On prend la longueur totale (a + b) = 1 † Le l'équation au-dessus de la figure (1) peut alors s'écrire :
La solution positive pour cela est :
La partie longue (a) représente donc un peu moins de 62 % de la longueur totale du segment de ligne. Et parce que b =1 – a , s'applique également :
Cela signifie que la partie courte (b) représente environ 38 % de la longueur totale du segment de ligne. Avec ces résultats on calcule le nombre d'or (phi :φ) avec la relation (1) :
Notez que le nombre 1,618 est exactement supérieur d'une unité à 0,618. C'est très bien pour quelqu'un qui aime les chiffres.
Le mathématicien Léonard de Pise a vécu d'environ 1170 à environ 1250. Il est également connu sous le nom de Fibonacci. Il a publié une série de nombres dans laquelle on retrouve subtilement le nombre d'or φ. La règle suivante s'applique dans la suite de Fibonacci :
a1 , a2 , un3 , un4 , ... avec un1 + a2 =un3 , a2 + un3 =a4 , ...
Chaque nombre est donc égal à la somme des deux nombres précédents. En partant des nombres 0 et 1, on obtient la suite de Fibonacci :
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ...
Si vous divisez deux membres consécutifs de la séquence, le résultat se rapproche de plus en plus du nombre d'or φ. Ceci est indiqué dans le tableau (1).
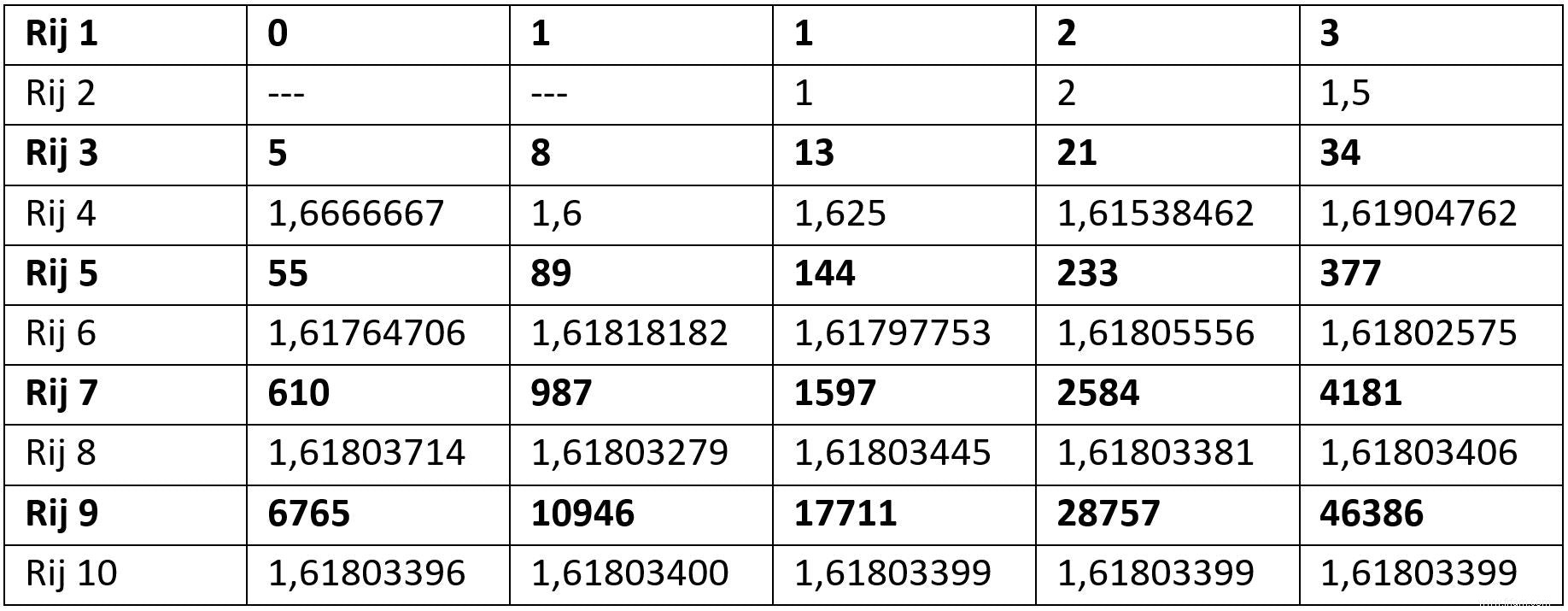
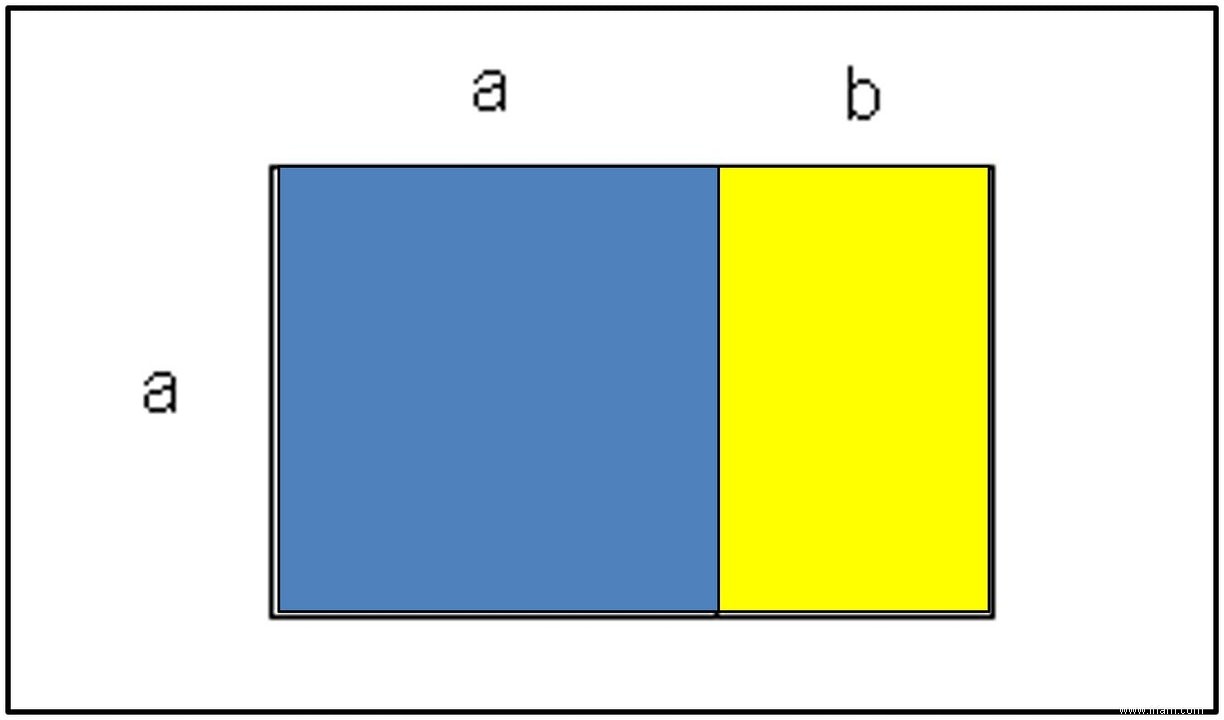
Ici, nous utilisons le fait que les rapports des nombres dans la séquence de Fibonacci (voir tableau 1) sont proches du nombre d'or. Par exemple, prenons un rectangle dont le côté long est égal à a + b = 8 + 5 =13 et petit côté égal à a =8 .
Pour couper ce rectangle d'une manière dorée, des nombres comme 8 et 13 doivent être deux nombres consécutifs dans la suite de Fibonacci. Le nombre d'or de la figure (2) divise le rectangle (13 X 8) en un carré bleu (8 X 8) et un rectangle jaune (8 X 5). Le carré a deux côtés égaux dont les longueurs ne sont pas deux nombres consécutifs dans la suite de Fibonacci. Le carré n'est donc pas éligible pour une prochaine distribution dorée.
Le plus petit rectangle a des côtés dont la longueur peut aller jusqu'à deux nombres consécutifs dans la suite de Fibonacci. Le rectangle jaune peut donc être encore coupé avec le nombre d'or. Le rectangle (8 X 5) est maintenant divisé en un carré (5 X 5) et un rectangle (5 X 3). Le carré (5 x 5) ne peut pas être divisé par un nombre d'or. Les chiffres ne sont pas deux nombres consécutifs dans la suite de Fibonacci, mais le rectangle (3 X 5) le peut. Et ainsi de suite, jusqu'à ce que nous nous retrouvions avec deux carrés (1×1) :également deux nombres consécutifs dans la suite de Fibonacci. Tout cela est illustré sur la figure (3)
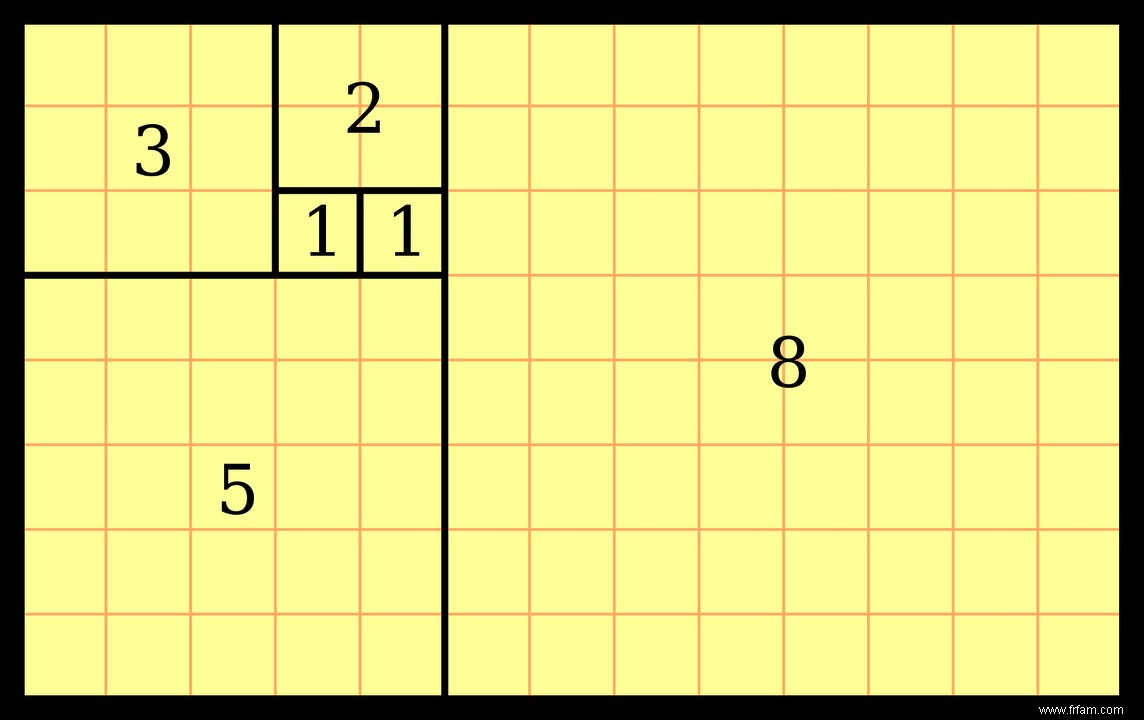
Par exemple, prenons un rectangle avec un côté long égal à 89 et un côté court égal à 55. Deux nombres consécutifs dans la suite de Fibonacci. Ce rectangle peut être divisé d'une manière dorée en 10 carrés avec des longueurs respectives de leurs côtés égales à 55, 34, 21, 13, 8, 5, 3, 2, 1 et 1. Ceci est montré dans la figure (4) ci-dessous.
Dessinez maintenant de A à B un quart de cercle de rayon 55. Continuez doucement de B à C le long d'un quart de cercle de rayon égal à 34. Continuez ainsi avec des quarts de cercle de rayons consécutifs égaux à 21, 13, 8, 5, 3, 2 et deux fois 1. Parce que les deux derniers quarts de cercle ont le même rayon et s'écoulent sans à-coups l'un dans l'autre, la dernière partie de la construction est un demi-cercle de rayon égal à 1. La construction ainsi réalisée est la Spirale ou la Cochlée de Fibonacci .

Comme mentionné précédemment, le concept du nombre d'or a été utilisé par les artistes et les architectes pendant des siècles, avant même qu'il ne soit fixé mathématiquement. On prétend même que les anciens Égyptiens utilisaient le principe dans la construction de leurs pyramides. Nous aimons donc conclure :qui cherche, trouve. le nombre d'or peut être trouvé partout dans le monde. Vous trouverez ci-dessous quelques exemples.

Le Parthénon
Ci-dessus, la façade du Parthénon. Elle a bravé les siècles, les guerres et l'irrespect sur 8 piliers. Pas 7 ou 9, mais 8. Un nombre de la suite de Fibonacci. La façade a un rapport de (21 X 13) et a donc été conçue pour être divisée en sept carrés de manière dorée. Avec des longueurs des côtés égales respectivement à 13, 8, 5, 3, 2, 1 et 1, entre 447 et 737 avant notre ère, les architectes et sculpteurs de l'édifice l'ont voulu. Les maîtres des travaux, bien sûr, ne connaissaient pas la séquence et le nombre de Fibonacci. Mais ils savaient que ces proportions dans un bâtiment sont un régal pour les yeux. Et que le puzzle recouvrant le rectangle (21 x 13) de 7 cases garantit également une stabilité maximale de la structure.
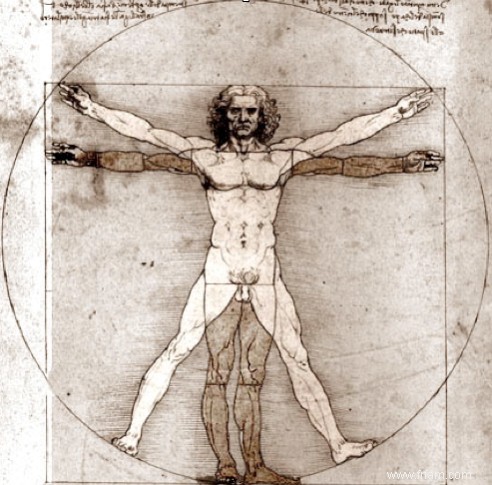
Léonard de Vinci et l'Homme de Vitruve
Le polyvalent romain Vitruve (architecte, ingénieur, ingénieur hydraulique, physicien, mathématicien, expert en anatomie humaine, ...) avait servi comme général sous Jules César. Il était d'abord architecte. L'une de ses principales propositions était que la longueur, la largeur, la hauteur et la profondeur d'un bâtiment devaient refléter les proportions du corps humain. Vitruve a été tiré de l'oubli par Léonard de Vinci peut-être encore plus polyvalent et très apprécié. Léonard a créé le célèbre "homme de Vitruve" vers 1490. Qui s'inscrit exactement dans un cercle et un carré. La longueur du côté du carré est exactement égale au rayon du cercle multiplié par le nombre d'or φ, comme le montre la figure (6). Il est absolument certain que Léonard connaissait à fond et appliquait le nombre d'or. Dans ce cas, la visée mathématique et esthétique conjointe est évidente.

Léonard de Vinci et la Joconde
Jusqu'à présent, cette histoire s'est bien déroulée. Une mathématique simple et élégante a conçu de manière étanche des bâtiments et des œuvres d'art qui ont traversé des millénaires et préservé leur beauté pour l'éternité. Il est entendu ici qu'il faut toujours commencer par des rectangles dont la largeur et la longueur ont comme dimensions deux nombres consécutifs de la suite de Fibonacci. Léonard a peint son énigmatique Mona Lisa entre 1503 et 1506. Dans ce tableau, Léonard s'est comporté comme un scélérat. Le tableau mesure 53 cm de large et 77 cm de haut. Sa farce est que 53 et 77 ne sont pas des nombres consécutifs dans la suite de Fibonacci.
Il devait savoir que cinq siècles après avoir peint la Joconde, de nombreuses personnes essaieraient de toutes les manières possibles de sonder la logique et la beauté de la peinture avec des nombres d'or et des spirales. Avec une largeur de 53 cm et une hauteur de 85,75 cm cela aurait été facile car 85,75/53 =1,618 = φ, et avec une hauteur de 77 cm et une largeur de 47,59 cm personne n'aurait dû chercher longtemps pourquoi la Joconde sourit si irrésistiblement car 77/47.59 =1.618 = .
Mais avec les dimensions réelles de la peinture étant de 53 cm de large et 77 cm de haut, toute tentative en termes de nombres d'or et de spirales n'est que pure spéculation. Le secret de la façon dont ses tours d'or fonctionnent vraiment, Leonardo s'est moqué de sa tombe. La figure (7) montre une partie du tableau. Dans cette section, le visage et le corps de la Joconde s'intègrent parfaitement dans un rectangle (21 X 13) divisé en 7 carrés. Cependant, le rectangle ne couvre qu'une partie du tableau dont les dimensions se moquent de la suite de Fibonacci. Dans le rectangle auquel Fibonacci obéit, la spirale va de ses mains au bout de son nez où deux (1 X 1) carrés clôturent le jeu mathématique. La spirale qui coule sur son visage un peu plus tôt transforme son sourire en une lumière parfaite. Léonard n'était probablement pas du tout un scélérat lorsqu'il a peint la Joconde. Du moins pas comparé au nombre d'or.

Le tournesol
Dans la distribution des graines dans un tournesol, la figure (8) montre des spirales qui tournent dans le sens des aiguilles d'une montre, tandis que d'autres tournent dans le sens inverse des aiguilles d'une montre. La taille du tournesol détermine le nombre de spirales. Habituellement, vous comptez 34 spirales pointant dans un sens et 55 se tordant dans l'autre sens. Avec des tournesols plus petits, vous vous retrouvez souvent avec 21 spirales qui tournent dans une direction et 34 qui vont contre ce fil. Les paires (34.55) et (21.34) contiennent toutes deux deux nombres consécutifs de la suite de Fibonacci.