Le 10 décembre, Roger Penrose, presque 90 ans, recevra le prix Nobel de physique à Stockholm. Mais sa lumière va bien au-delà des trous noirs et des singularités spatio-temporelles. Nous pensons que Penrose est éligible pour au moins trois autres prix, malheureusement non inclus dans les spécifications de l'Académie royale des sciences de Suède.
Début octobre, on apprenait que le mathématicien et physicien britannique Roger Penrose recevrait la moitié du prix Nobel de physique le 10 décembre à Stockholm. Monsieur Penrose, comme on peut l'appeler depuis 1994, a montré que les mystérieux trous noirs de notre univers ne sont pas seulement dans les têtes obscures des Trekkies existent, mais qu'elles peuvent théoriquement être dérivées de la relativité générale. L'autre moitié des 10 millions de couronnes suédoises ira à l'astrophysicien Reinhard Genzel et à l'astronome Andrea Ghez, qui à leur manière ont prouvé l'existence de trous noirs, à savoir simplement en en trouvant un, en particulier l'étourdisseur Sagittaire< A*, au centre de la Voie lactée, plus de 4 millions de fois la masse de notre soleil. Mais les mathématiciens étaient déjà convaincus de l'existence de ces phénomènes obscurs depuis la publication de Penrose en 1965, dont voici une illustration dessinée à la main qui rend son idée claire d'un coup d'œil (?) :
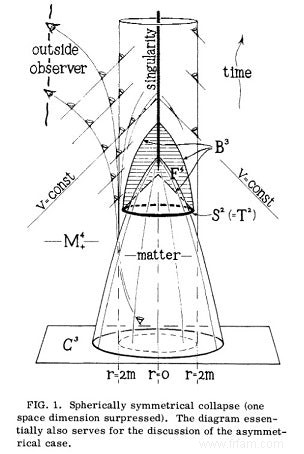
Pourtant, la lumière de Roger Penrose, qui a maintenant presque 90 ans, va bien au-delà de ces trous noirs, bien au-delà des singularités spatio-temporelles et de l'origine de l'univers (conseil de lecture :Cycles of Time :An Extraordinary New Vue de l'Univers à partir de 2010), et même au-delà de la collaboration magique avec Stephen Hawking (Conseil de lecture :The Nature of Space and Time à partir de 1996). En effet, nous pensons qu'il est éligible pour au moins trois autres prix, s'ils devaient jamais être décernés par l'Académie royale des sciences de Suède :

Un autre court-circuit d'enregistrement visuel dans le cerveau est causé par le piège de Penrose :
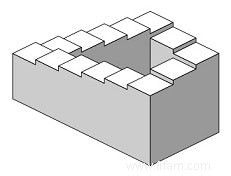
Cette ascension perpétuelle a à son tour inspiré Escher, par exemple dans l'estampe lithographique suivante de 1960 :


La surface est remplie de carreaux de la même forme, sans chevauchement et sans lacunes, comme on pourrait s'y attendre pour le sol de notre cuisine ou le mur de notre salle de bain. Parfois, deux ou plusieurs formes de tuiles sont également utilisées, comme on peut l'admirer abondamment à l'Alhambra (Grenade) :

Par pitié pour le carreleur, mais aussi parce que c'est plus silencieux pour le spectateur, la plupart des motifs de carreaux sont périodiques † Cela signifie que le motif se répète si vous le déplacez dans une certaine direction. Nous aimerions renvoyer le lecteur intéressé à notre article de blog précédent sur les mosaïques, ou à la signification de celle-ci en un mètre et demi. Depuis l'été 2017, nous connaissons toutes les tuiles polygonales convexes qui nous permettent de remplir le plan sans utiliser de multiples formes. Heureusement pour les carreleurs, tous ces motifs de tuiles s'avèrent être périodiques. On ne sait toujours pas s'il existe des motifs de pavage non périodiques avec une tuile, qui doit nécessairement être de forme plus complexe qu'un polygone convexe.
Mais on s'en écarte. En 1974, Roger Penrose a découvert un ensemble de deux carreaux simples en forme de losange, et un motif dans lequel les deux sont combinés pour remplir parfaitement la surface :
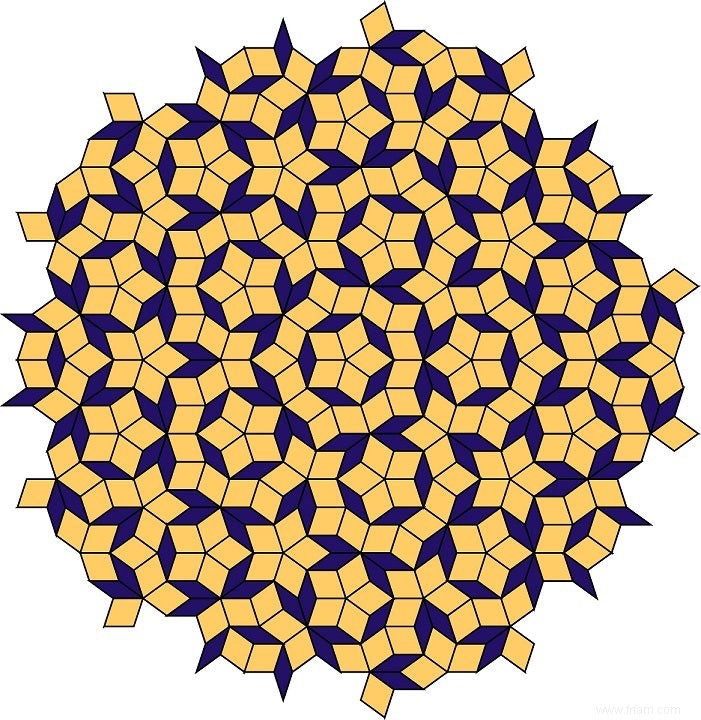
La particularité de ce motif est qu'il n'est pas périodique et que vous ne pouvez jamais trouver de pavage périodique avec ces deux formes. De plus, c'était la première fois qu'un motif de pavage pour des carreaux polygonaux à symétrie quintuple était trouvé.
Onze ans après cette découverte, lorsque les microscopes électroniques étaient suffisamment développés, ce même motif de Penrose a été observé dans un quasi-cristal :

Comment ne pas être impressionné par l'esprit visionnaire de Sir Roger Penrose ? Utilisant une perspicacité purement mathématique, il prouva l'existence de trous noirs dans l'univers et inventa la symétrie des quasi-cristaux de nombreuses années avant que les scientifiques empiriques ne les observent. Quand nos appareils de mesure seront-ils suffisamment avancés pour détecter également ses autres fantasmes (notre conscience quantique, le triangle impossible,...) ?