Boire beaucoup est le message, par temps chaud. Et assurez-vous de toujours prendre un verre avec vous. Une tasse pas trop lourde que vous pouvez remplir d'une quantité infinie d'eau est idéale pour cela. Une vision mathématique de la question.
Evangelista Torricelli (1608-1647) est surtout connu pour sa flûte et sa trompette. Vous pouvez voir ce dernier dans l'image en haut de ce blog. La trompette de Torricelli (également appelée cor de Gabriel) est une chose paradoxale. C'est une surface de révolution créée en faisant tourner un morceau d'une hyperbole autour d'une de ses asymptotes. Le résultat est une surface dont on peut calculer le volume, et aussi la surface du manteau :la surface de la surface elle-même. Notez que la trompette continue indéfiniment.
Torricelli a prouvé en 1641 que la surface du manteau est infiniment grande, mais que le volume est fini. Cela a frappé fort à l'époque, car on pensait qu'une telle chose était impossible :si la chose est infiniment grande, alors le contenu ne peut pas être fini. Les illustres contemporains de Torricelli furent d'abord convaincus qu'il avait tout simplement mal calculé. Le philosophe Thomas Hobbes (1588-1679) a même dit à cet égard :Pour comprendre cela comme sens, il n'est pas nécessaire qu'un homme soit géomètre ou logicien, mais qu'il soit fou.
La trompette de Torricelli donne lieu au célèbre paradoxe du peintre :

Supposons que vous vouliez peindre l'intérieur de la trompette, alors cela semble impossible car la surface qu'il vous reste alors à peindre est infiniment grande. Mais qu'en est-il de la prochaine alternative ? Posez la trompette sur le côté et remplissez-la complètement de peinture (contenu =finition !). Puis l'intérieur est soudainement peint, n'est-ce pas ?
On peut aussi voir ainsi la trompette comme une sorte de coupe, infiniment grande mais de volume fini. Ce n'est donc pas exactement ce que nous recherchons. Après la découverte de Torricelli, René François Walter de Sluse (1622-1685), mathématicien liégeois, et Christiaan Huygens (1629-1695) s'associent et partent à la recherche d'autres miracles de ce type.

Pour ce faire, ils ont étudié les propriétés d'une courbe connue depuis l'Antiquité :la cissoïde de Dioclès, déjà décrite vers 200 avant J.-C. par le mathématicien grec Dioclès. Dioclès a étudié la courbe car elle lui a permis de résoudre l'un des problèmes déliens, à savoir le dédoublement du cube :
pour se débarrasser de la peste, la légende raconte que les habitants d'Athènes devaient demander au dieu Apollon leur de doubler l'autel en son honneur. Ils firent un nouvel autel aux côtés deux fois plus longs qu'auparavant, mais la peste s'aggrava :Apollon n'était pas satisfait. L'intention était en effet qu'ils doublent le volume de l'autel, et vous faites cela en multipliant les côtés par $\sqrt[3]{2}$.
Ici vous voyez un dessin du cissoïde, qui est défini par un cercle tangent à une ligne :

Les points de la cissoïde sont définis comme suit. Une droite passant par le point $O$ coupe le cercle au point $M_1$ et la droite donnée au point $M_2$. Le point $M$ de la cissoïde qui se trouve sur cette ligne est choisi de sorte que la distance de O à $M_1$ soit égale à la distance de $M$ à $M_2$.
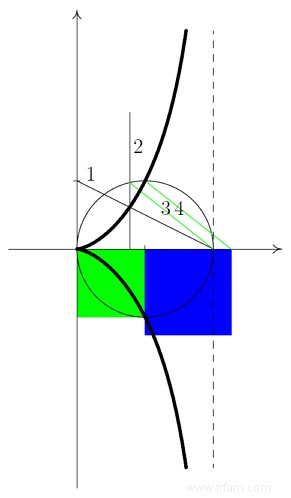
Pour montrer comment faire le dédoublement du cube avec cette courbe, prenons un carré de côté 1 (en vert sur la figure), un cercle de rayon 1 tangent à la ligne pointillée sur la figure, et construisons la cissoïde qui lui appartient cercle et cette ligne.
Et puis nous continuons comme indiqué sur la figure. Tracez successivement les lignes numérotées 1, 2, 3 et 4 et l'intersection de la ligne 4 avec l'axe horizontal permet de construire le carré bleu de côté $\sqrt[3]{2}$.
Huygens et les Sluse pensaient qu'avec le cissoïde vous aviez quelque chose de similaire à la surface de Torricelli. Notez qu'à cette époque, le calcul de volumes et de surfaces déterminés par des courbes était un sujet brûlant, sur lequel il y avait beaucoup de correspondance. En effet, la coopération entre Huygens et de Sluse se faisait par lettre. Vous voyez ici un fragment de la lettre que Huygens a écrite aux Sluse le 28 mai 1658.

Vous pouvez également voir une partie du cissoïde dessinée. Ils ont découvert que si vous faites pivoter la partie de surface orange (voir figure suivante) entourée par la cissoïde, l'asymptote et l'axe horizontal autour de son asymptote, que le volume est en effet finiment grand. Mais en plus, pensa de Sluse, si vous faites pivoter cette partie de la surface (voir figure en bleu) autour de l'axe vertical, le contenu est également de taille finie !

Le résultat est une tasse qui ressemble à ceci :

La coupe, que l'on appelle parfois aussi le vase de la Sluse, s'étend à l'infini, elle est infiniment haute. Mais vous n'avez besoin que d'une quantité finie de matériel pour le fabriquer ! Et il peut contenir une quantité infinie. De Sluse lui-même l'exprime ainsi, dans sa lettre à Huygens du 12 avril 1658 :... pondere non magni, quod interim helluo nullus ebibat. (La tasse ne pèse pas beaucoup, mais le plus gros buveur ne la videra pas.)
Donc :idéal par temps très chaud. (Pour votre information, au moment de la rédaction de ce blog, nous mesurons des températures de 35 $^{\circ}$C.)