"Ajouter un hôpital tous les quelques jours" est beaucoup moins dramatique que "doubler le nombre d'admissions". Le mathématicien Dirk Huylebrouck explique également le risque d'une croissance exponentielle.
Le 23 octobre, un journal de qualité l'imprime en gros titre :« Un hôpital en plus chaque jour ». À première vue, il semble qu'elle ait cité le virologue Steven Van Gucht, qui avait déclaré ce qui suit à propos du nombre d'admissions à l'hôpital la veille :"Tous les dix jours, nous constatons un doublement dans ce domaine". Ce n'est pas tant le nombre de jours, mais la manière dont la croissance est décrite qui pose problème :si l'on rajoute et repasse une quantité constante, ce n'est pas la même chose que si l'on double sans cesse une quantité. "Ajouter un hôpital" tous les quelques jours, c'est beaucoup moins dramatique que "doubler le nombre d'admissions".
Dans un Eos blog, la philosophe Sylvia Wenmackers a fait la comparaison avec l'intérêt composé :"Aussi petit que soit le pourcentage de base, s'il est ajouté quelque part à des moments précis, le total augmente de façon exponentielle". Elle parle désormais aussi de comptage "supplémentaire", mais cela dépend à quoi s'applique ce pourcentage de base. Avec un pourcentage sur le même montant de base, on parle d'intérêt simple; avec un pourcentage sur le montant de base plus les intérêts accumulés, vous obtenez effectivement des intérêts composés. Supposons, comme dans ce blog, que vous ayez 100 euros et que vous receviez 1 % d'intérêts par an. Simple devient l'intérêt et le montant total sur différentes années :1 et 100+1=101 ; 1+1=2 et 100+2=102 ; 2+1=3 et 100+3=103 ; et ainsi de suite, mais composé c'est 1 et 100+1=101; 101×0,01=1,01 et 101+1=102,01; 102,01×0,01=1,0201 et 102,01+1,0201=103,0301 ; et ainsi de suite... Dans le premier cas c'est « quelque part » dont on prend toujours le pourcentage de base de 100, mais dans le second c'est 100; 101 ; 102.01 ; et ainsi de suite. Et c'est toute une différence, comme l'a expliqué Sylvia Wenmackers.
J'ai moi-même tenté d'expliquer cette croissance exponentielle sur la base d'une description qu'Al Gore utilisait déjà dans son documentaire sur le changement climatique, « Une vérité qui dérange » :elle suit une « courbe en crosse de hockey ». Le manche d'un bâton de hockey sur glace posé à plat suit à peu près l'axe horizontal, mais la partie avec laquelle le palet est renversé s'élève rapidement verticalement. Parce qu'une rondelle de hockey sur glace est généralement frappée fortement, cela donne une belle image presque cinématographique pour une telle courbe exponentielle :elle "tire" très rapidement, pour ainsi dire, après une partie initialement presque horizontale.
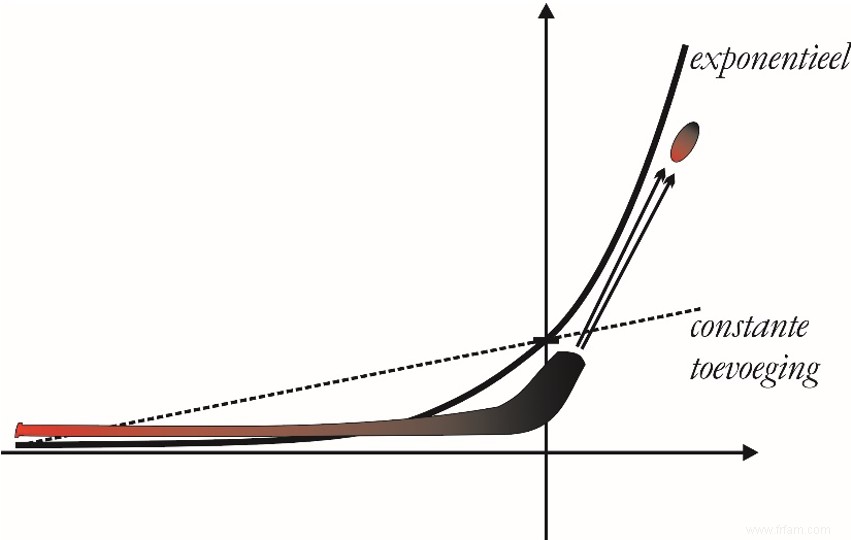
Et en effet, un virus se multiplie donc selon un processus exponentiel, comme j'ai tenté de l'illustrer dans l'article cité plus haut en utilisant des grains de riz sur un échiquier. Si leur nombre continue de doubler, 1 grain sur la première case donnera 2, puis 2²=4, puis 2³=8, puis 16, puis 32, et ainsi de suite, jusqu'à ce qu'un nombre imprononçable soit atteint sur la case 64.

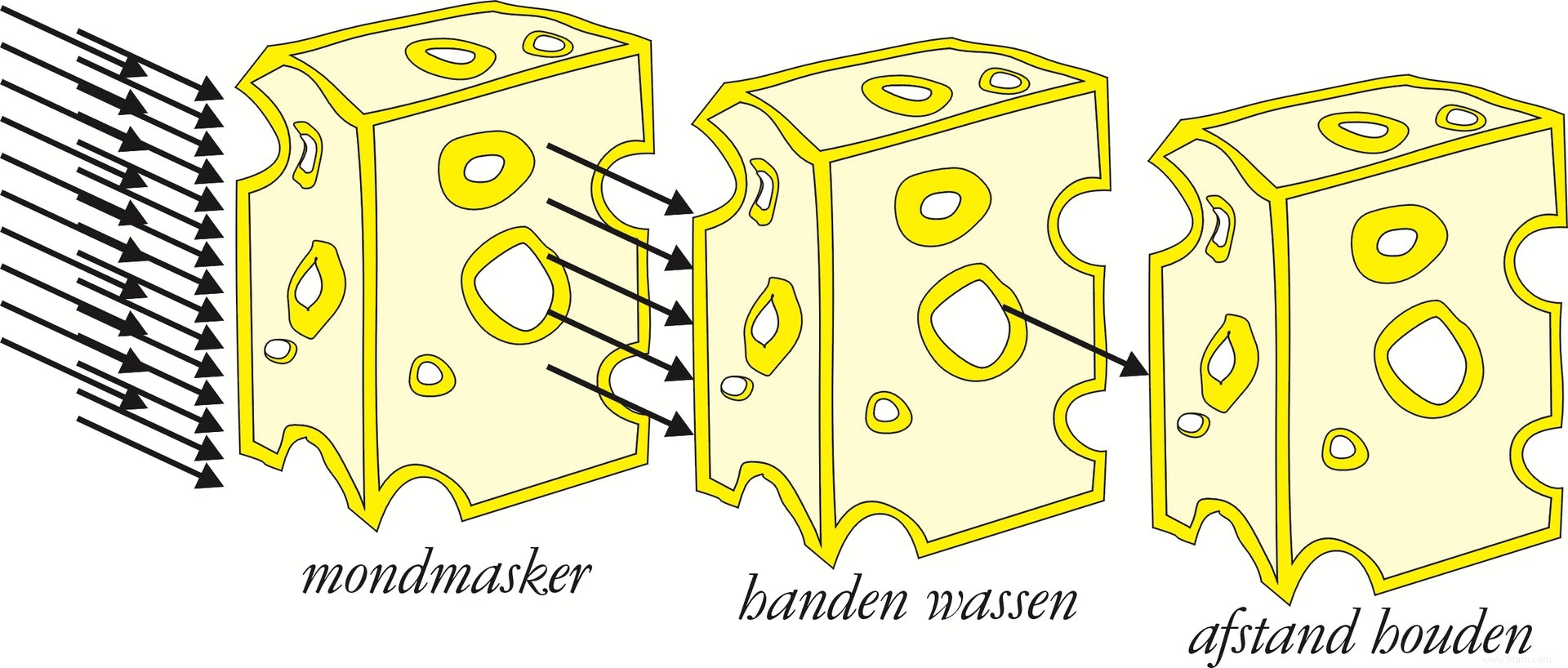
D'un autre côté, cela contient aussi la bonne nouvelle :supposons qu'un masque buccal n'arrête que 4/5 des virus. Puis une partie 1/5 arrivera, comme le prétendent certains fervents critiques. Supposons maintenant que le lavage des mains n'arrête que 4/5 des coronaatjes. Puis 1/5 revient. Ces chiffres sont toujours purement hypothétiques, et estimés à la hausse, pour accommoder les critiques. Et gardez vos distances, précisons aussi que cela n'est efficace que pour les 4/5. L'effet total est alors que (1/5)³ des virus pénètrent toutes les barrières, soit 0,008 =0,8 %. C'est presque rien, malgré les valeurs estimées élevées, car les différentes barrières suivent également un processus exponentiel. En combinant différentes mesures, nous pouvons donc utiliser cette maudite courbe exponentielle du virus contre elle-même.