La loi de Stigler proclame qu'une invention, une formule ou un principe porte généralement le nom de la mauvaise personne, et non du découvreur. On en trouve de nombreux exemples dans les nombres complexes. Une raison pour nous d'apporter l'histoire des nombres complexes.
La loi de Stigler proclame qu'une invention, une formule ou un principe porte généralement le nom de la mauvaise personne, et non du découvreur. Par exemple, la loi de Stigler s'applique au théorème de Pythagore, mais certainement aussi à elle-même. Parfois, les erreurs sont plus ou moins corrigées :par exemple, le nombre de Reynolds de la mécanique des fluides a en fait été introduit par George Stokes, et le théorème de Stokes a en fait été écrit par Lord Kelvin. Il y a rarement une véritable dispute sur les priorités, mais quand c'est le cas, nous le savons :pensez à la bataille entre les deux géants Newton et Leibniz.
Surtout dans l'histoire des nombres complexes La loi de Stigler a fait des ravages, et peut-être en savons-nous autant sur son origine parce qu'il y a eu pas mal de discussions pendant cette période. Le nombre complexe l'était d'après un enfant mort-né, rejeté par son découvreur comme le monstre de Victor Frankenstein par son créateur. Gérolamo Cardan (1501-1576) a découvert les nombres complexes lorsqu'il avait besoin de la racine carrée d'un nombre négatif comme étape intermédiaire dans ses calculs 
. Il a vu cela comme une torture mentale (sic), mais en calculant obstinément, il a quand même trouvé la bonne solution finale.
Mais en fait, il est plus correct de Rafael Bombelli comme le père des nombres complexes, car Bombelli les a en fait mis en scène comme des nombres (dans une série de trois livres, entre 1572 et 1579), ayant droit à l'addition et à la multiplication, et non une vilaine construction imaginaire comme le respectaient Cardano et d'autres contemporains.
La torture susmentionnée pour Cardano s'est produite dans un calcul intermédiaire pour résoudre une équation cubique, telle que $x ^ 3 =15x + 4 $, une équation typique qui apparaît dans les problèmes de calcul de volume. Cardano s'est avéré avoir besoin de $\sqrt{-121}$, c'est-à-dire une solution de l'équation $x^2+121=0$, comme vous pouvez le voir dans la formule de Cardano pour ce cas :$(p,q>0 )$
$$ x^3 =px + q \ \ \mbox{dan} \ \ \ x=\sqrt[3]{\frac{q}{2} + \sqrt{\frac{q^ 2} {4}-\frac{p^3}{27}}}+\sqrt[3]{\frac{q}{2} - \sqrt{\frac{q^2}{4}-\frac {p ^3}{27}}}$$
qui dans ce cas donne :$$ x=\sqrt[3]{2 + \sqrt{-121}}+\sqrt[3]{2 - \sqrt {-121}}.$$À une époque où un nombre négatif était déjà difficile à digérer, tirer sa racine carrée ne pouvait que provoquer un court-circuit. Jusque-là, les mathématiciens soutenaient que $x^2+121=0$ était simplement une équation impossible et n'avait pas de solution. Vous pourriez suggérer une bonne attitude, laisser les équations impossibles telles qu'elles sont et ne pas chercher les problèmes. Mais la chose étrange à propos du problème de Cardano était que son équation cubique originale avait une solution réelle, à savoir $x=4$, mais dans sa méthode, il était obligé de traiter des "inexistants" (imaginaires ) calcule des nombres, tels que $\sqrt{-121}$ 
. Par exemple, Cardano pourrait dire que $x^2+150=29$ 
car $x^2+121=0$ 
, mais il n'a pas compris ce qu'il faisait parce que $x$ ne l'a pas fait' t exister. Le fait que la formule ci-dessus pour résoudre une équation cubique est toujours la formule de Cardano est une belle illustration de la loi de Stigler. En effet, cette formule a été publiée pour la première fois en 1545 par Cardano dans son livre d'algèbre Ars Magna , mais Cardano avait appris la formule de Tartaglia , et avant cela la formule était probablement déjà connue de Ferro .
Cardano considérait probablement l'utilisation de racines imaginaires de nombres négatifs comme un défaut de la méthode elle-même et soupçonnait que quelqu'un découvrirait plus tard une méthode propre pour calculer les solutions réelles d'une équation cubique. Mais en 1843, Pierre Wantzel a prouvé que pour de nombreuses équations cubiques, il ne peut y avoir de formule qui calcule les solutions réelles sans rencontrer des racines carrées de nombres négatifs (le soi-disant casus irreducibilis † Ainsi, les nombres complexes se sont avérés ne pas être une solution de contournement, et les mathématiciens sont passés de l'acceptation du mal nécessaire à l'adoption du meilleur qui leur soit jamais arrivé. La déclaration suivante est illustrée par le mathématicien français Jacques Hadamard (1865 – 1963) est posée :
Le plus court chemin entre deux vérités dans le domaine réel passe par le domaine complex.
Mais la loi de Stigler ne s'applique nullement aux citations, cette affirmation devrait plutôt être au nom de Paul Painlevé...
Mais en fait, nous n'avons pas encore expliqué ce que sont les nombres complexes être. La graine de ces nouveaux nombres est l'unité imaginaire je , qui est entrée comme solution de l'équation $x^2+1=0$ 
. Puisque cette équation n'a pas de solution sur l'axe des nombres réels, nous ne pouvons pas représenter $i$ sur cet axe. Donc $i^2=-1$ 
. Si on applique les règles de calcul connues à ce nouveau nombre, alors $x^2+1=0$ tout de suite aussi une seconde solution puisque $(-i)^2=i^2 =-1$ 
. Nous avons donc deux racines carrées de $-1$ 
saisi :$\sqrt{-1}=\pm i$. Plus n'est nécessaire pour pouvoir calculer toutes les racines carrées des nombres négatifs, c'est-à-dire comme des multiples de l'unité imaginaire, par exemple $\sqrt{-9}=\pm 3i$ 
car $(\pm 3i)^2 =9 i^2 =-9 $ 
.
De plus, lorsque nous ajoutons ces nouveaux nombres imaginaires aux "anciens" nombres réels, nous obtenons des hybrides comme $5-3i, 1+i$, 
etc., et tout cela devient des nombres complexes Nommé. Un nombre complexe $z=a+b i$ 
peut sembler virtuel, mais il est constitué de deux composants réels :$a$ (la partie réelle de $z $ ) et $b$ (la partie imaginaire de $z$). Ainsi, les nombres réels sont des nombres complexes spéciaux avec une partie imaginaire égale à 0, et les racines des nombres négatifs mentionnés ci-dessus sont des nombres complexes avec une partie réelle égale à 0.
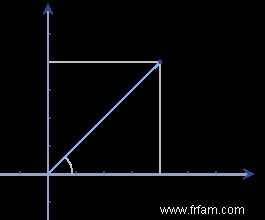
Ainsi, les nombres complexes ajoutent une composante imaginaire aux nombres existants, et nous pouvons imaginer cela comme une dimension supplémentaire à l'axe des nombres réels. Cela nous amène à la visualisation des nombres complexes dans le plan complexe :
Cette représentation géométrique est devenue particulièrement populaire depuis le grand mathématicien Carl Friedrich Gauss (1777-1855) en répandent l'usage. Immédiatement, les nombres complexes sont sortis de la sphère taboue. En effet, dès que les gens peuvent imaginer quelque chose (visuellement), cela existe réellement. À ce jour, nous appliquons ici la loi de Stigler et appelons cette représentation des nombres complexes le plan de Gauss , alors que cette représentation géométrique a déjà été utilisée par des mathématiciens tels que Wessel et Argand †
Les constructions géométriques et les formules trigonométriques se sont soudainement révélées beaucoup plus simples grâce au produit complexe. Un exemple classique de cela est la formule de De Moivre :$$\cos n\theta + i \sin n\theta =(\cos \theta + i \sin \theta)^n.$$Cependant, Abraham De Moivre a écrit (1667 - 1754) que son ami Newton avait déjà utilisé cette formule dans ses calculs (1676), mais la loi de Stigler n'en était pas gênée. D'autre part, Newton a obtenu de l'histoire le mérite du binôme de Newton , alors que cette formule était connue depuis longtemps des Arabes.
Les physiciens et les ingénieurs ont également fait bon usage des nombres complexes dans les calculs des ondes et des vibrations, ou des réseaux électriques. Dans l'ensemble, cependant, les nombres complexes sont les plus appréciés dans le domaine où ils sont apparus pour la première fois, à savoir l'algèbre. Après tout, ils fournissent un cadre parfait et complet pour toutes les opérations algébriques :somme, différence, produit, division, puissances et racines. En introduisant simplement $i$ (comme racine carrée de $-1$), nous pouvons maintenant calculer toutes les racines carrées à partir de nombres négatifs et aussi toutes les racines supérieures. De plus, nous recevons le cadeau que chaque équation polynomiale a des solutions comme nombres complexes, même si nous sommes autorisés à choisir les nombres complexes comme coefficients, alors que nous n'avons ajouté que la solution de $x^2+1=0$. C'est le théorème principal de l'algèbre † Par exemple l'équation $x^2-2x+2$ n'a pas de solutions réelles en raison d'un discriminant négatif. Mais vous pouvez calculer que $(1+i)^2-2(1+i)+2=0$ 
. Donc, si nous quittons notre axe des nombres réels et enrichissons nos nombres avec une partie imaginaire, nous trouvons une solution, qui est $1+i$ . L'autre solution de cette équation est donnée par $1-i$ . En raison de la loi de Stigler, le théorème fondamental de l'algèbre est généralement attribué à d'Alembert , bien que sa preuve en 1746 soit incomplète. La première preuve complètement irréprochable est probablement celle d'Argand, bien que de nombreux étudiants en mathématiques l'apprennent comme la preuve de Cauchy (qui a été le premier à le publier dans un manuel, mais sans citer la source).
La success story des nombres complexes, qui a commencé avec l'horreur de Cardano, lorsqu'il a dû calculer avec des racines imaginaires, nous fait involontairement penser au vilain petit canard, un conte de fées de Hans Christian Andersen (ou était l'idée de quelqu'un de la métamorphose en cygne par quelqu'un qui pensait différemment ?).
