Saviez-vous que...
... aujourd'hui est $\boldsymbol \pi$ jour ? Pourquoi? Parce que dans l'orthographe américaine la date du 14 mars s'écrit 3/14 et 3.14 est une approximation du nombre $\pi$.
... depuis le 26 novembre 2019 grâce à l'UNESCO :
... le record européen de mémorisation décimale de $\pi$ depuis le 7 mars 2020 est détenu par le Suédois Jonas von Essen (29 ans), avec 24063 décimales ? Depuis 2015, le record du monde est détenu par l'Indien Suresh Kumar Sharma (aujourd'hui âgé de 24 ans), avec 70030 décimales.
... le record $\pi$ de novembre 2016 depuis la journée $\pi$ précédente a déjà été battu deux fois ? En 2016, Peter Trüb a calculé $\pi^e$ billions de décimales à partir de $\pi$. Soit 22 459 157 718 361 chiffres. L'ordinateur a commencé le calcul le 29 juillet et l'a terminé le 11 novembre 2016.
En comparaison, en 1946, l'ENIAC, le premier véritable ordinateur électronique, calculait 2 037 décimales de $\pi$ en 70 heures.
La formule de Machin a été utilisée :$$\frac{\pi}{4} =4 \cdot {\rm Bgtg} \frac{1}{5} - {\rm Bgtg} \frac{1}{239} .$ $

... le $\pi$ day 2019, il a été annoncé qu'Emma Haruka Iwao, Developer Advocate chez Google, avait calculé 31 415 926 535 897 (soit 31,4 billions) de décimales de $\pi$ dans le cloud. Temps de calcul :121 jours.
Le 29 janvier 2020, le calcul (et la vérification) par Timothy Mullican des 50 000 milliards de décimales de $\pi$ a pris fin. Le calcul a pris 303 jours. Pour les deux enregistrements, la formule des frères Chudnovsky a été utilisée :$$ {1\over\pi}=12\sum_{k=0}^{\infty}{(-1)^k(6k)!\over( 3k )!(k!)^3} {13591409+545140134k\about 640320^{3k+3/2}} .$$
...dans le tristement célèbre procès d'O.J. Simpson, la crédibilité du témoin du FBI, l'agent spécial Roger Martz (un chimiste du FBI Forensic Science Research Unit, à Quantico) a été mise en doute parce qu'il était incapable de donner la valeur du nombre $\pi$?
Caricature de Tegan Phillips :

... M38 est un grand amas d'étoiles dans la constellation Auriga (Carter) où dans la constellation des étoiles les plus brillantes vous reconnaîtrez la lettre grecque $\pi$ ? Et qu'en 1995, Robert Matthews a utilisé la position des étoiles dans le ciel pour trouver une approximation de $\pi$ (titre publié :Pi dans le ciel) ?
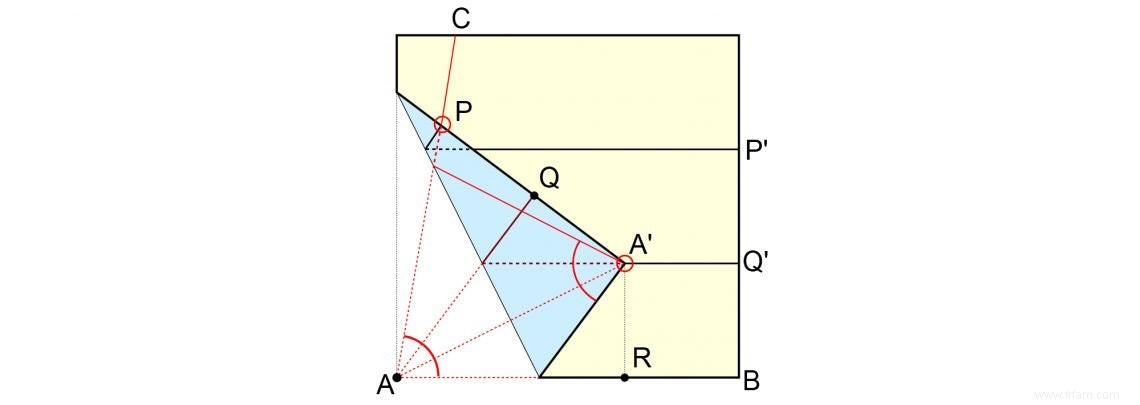
... des trois anciens problèmes déliens (utilisant uniquement le compas et la règle (1) pour diviser un angle en trois parties égales, (2) pour doubler un "cube", c'est-à-dire pour construire $\sqrt[3]{2}$ et ( 3) construire le nombre $\pi$) unique (3), également appelé la quadrature du cercle mentionné, n'est pas résoluble avec l'origami? Ci-dessous, vous pouvez voir une solution pour (1).
Que j'aime à faire apprendre ce nombre utile aux sages !
Immortel Archimède, artiste ingénieur,
Qui de ton jugement peut prendre la valeur ?
Pour moi, ton problème coupe de pareils avantages.
Jadis, mystérieux, un problème bloquait
Tout l'admirable process, l'œuvre grandiose
Que Pythagore découvrit aux anciens Grecs.
0 quadrature ! Vieux tourment du philosophe
Insoluble rondeur, trop longtemps vous avez
Défié Pythagore et ses imitateurs.
Comment intégrer l'espace plancirculaire ?
Former un triangle auquel il équivaudra ?
Nouvelle invention :Archimède inscrira
Dedans un hexagone; appréciera son aire
Fonction du rayon. Pas trop ne s'y tiendra :
Dédoublera chaque élément antérieur ;
Toujours de l'orbe calculé approchera ;
Définir la limite ; in the end, l'arc, le limiteur
De cet inquiétant cercle, ennemi trop rebelle
Professeur, enseignez son problème avec zèle
C'est un indice.
Une chaîne qui ne se répète ni ne se termine jamais, le catalogue total intemporel,
des séquences insaisissables, la somme de l'univers.
Cette énigme de la nature demande :
La totalité ne peut-elle voir aucun modèle, révélateur l'ordre comme déguisement de la réalité ?
Il était une fois une fille qui aimait pi
Je n'ai jamais compris pourquoi
Pour elle c'est une merveille
Pour moi juste un chiffre
Sa beauté révélée par et par
(Tom Wilson)
Picasso, malgré son nom, n'a pas fait de peinture du nombre $\pi$, mais que d'autres artistes se sont inspirés de $\pi$ (par exemple Squared Circle (1968), Crockett Johnson) ?
