Vous avez sans doute déjà vu le graphique qui est massivement partagé sous le slogan « aplatir la courbe ». Les blogueurs Simon Telen et Andreas Van Barel expliquent la base mathématique du modèle.
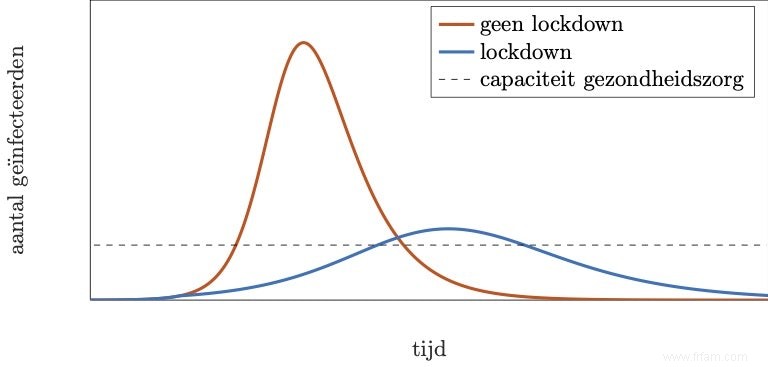
Ce graphique, parfois appelé «courbe corona», montre le nombre de personnes infectées en fonction du temps. Si nous n'agissons pas, nous suivrons la courbe rouge. Trop de personnes tombent alors malades en succession rapide, ce qui signifie que la capacité du système de santé est dépassée. L'idée de la distanciation sociale, du télétravail et d'autres mesures similaires est de ralentir la propagation de la maladie. Cela se traduit par la courbe bleue. Moins de personnes devront alors être admises dans les hôpitaux en même temps afin que la plupart (et dans le meilleur des cas tous) les patients aient encore une place. Mais comment arrive-t-on réellement à ce graphique ? Pourquoi le nombre d'infections augmente-t-il si rapidement en premier lieu ? Pourquoi ce nombre finirait-il par baisser, si le virus est si contagieux après tout ?
Pour répondre à ces questions, nous discutons d'un modèle très simplifié décrivant la propagation des maladies infectieuses. Connu sous le nom de modèle SIR, ce modèle divise la population en trois groupes :
1. Groupe S d'individus sensibles. Ils n'ont jamais eu le virus mais peuvent éventuellement être infectés.
2. Groupe I de personnes infectées. Ils ont le virus et peuvent infecter les personnes du groupe S.
3. Groupe R de personnes guéries ou décédées. Ils avaient la maladie, mais ont depuis été guéris ou sont morts. Ils ne peuvent plus contracter la maladie. Nous supposons donc que lorsque vous guérissez, vous devenez immunisé contre la maladie.
Les noms des groupes viennent de l'anglais « susceptible », « infective » et « récupéré ».
Scheme can nous proposons le modèle SIR comme suit.

Pour comprendre comment la courbe corona émerge du modèle, nous devons spécifier à quelle vitesse les personnes du groupe S se retrouvent dans le groupe I, et les personnes de I se retrouvent dans le groupe R. Selon le modèle SIR, la transition de S à I se produit plus rapidement lorsqu'il y a plus de personnes dans le groupe I. En effet, plus il y a de personnes déjà malades et donc capables d'en infecter d'autres, plus la maladie se propagera rapidement. La facilité avec laquelle une personne infectée peut transmettre le virus est en outre déterminée par un paramètre que nous appellerons $\beta$. Ce paramètre indique combien d'autres personnes sont exposées à la maladie par jour par une personne infectée. Cependant, toutes les personnes exposées ne sont pas sensibles à la maladie. Rien ne change pour les personnes déjà atteintes de la maladie (groupe I). Les personnes qui ont déjà eu la maladie (groupe R) sont immunisées selon notre modèle. Seul le groupe S est sensible et ne représente qu'une fraction de la population totale. En conséquence, pour chaque personne infectée, en moyenne $\beta$ personnes par jour ne seront pas infectées, mais seulement $$\beta \times \frac{\text{nombre de personnes susceptibles}}{\text{nombre de personnes dans la population}}. $$ Nous concluons que chaque jour
$$ \beta \times \text{nombre de personnes infectées} \times \frac{\text{nombre de personnes susceptibles}}{\text{nombre de personnes dans la population}}$$
de nouvelles infections se produisent. En utilisant la notation courte $S$, $I$ et $R$ pour le nombre d'individus sensibles, infectés et immunisés et la lettre $N$ pour le nombre de personnes dans la population, cela donne le nombre $\beta I \frac{S}{N}$.
La deuxième transition est de I à R. La rapidité avec laquelle les gens guérissent ou meurent, bien sûr, varie d'une maladie à l'autre. Un deuxième paramètre $\gamma$ indique quelle proportion de personnes infectées I par jour guérit ou meurt. Chaque jour il y aura
$$
\gamma \times \text{nombre de personnes infectées} =\gamma I
$$
les individus du groupe I se retrouvent dans le groupe R. Avec ces informations, nous pouvons compléter la représentation schématique du modèle SIR pour
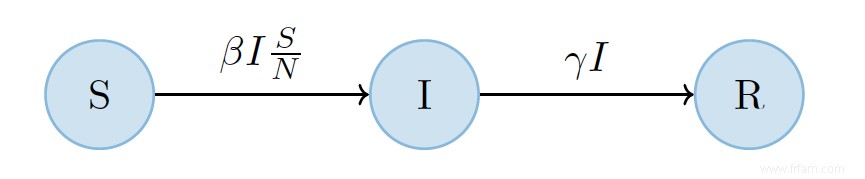
A l'aide de ce modèle simple, nous pouvons calculer avec l'ordinateur l'évolution de $S$, $I$ et $R$. Pour cela, nous avons besoin de valeurs pour $\beta$ et $\gamma$. Pour le moment, cependant, peu de données fiables sont disponibles, nous ne savons donc pas exactement $\beta$ et $\gamma$ pour le coronavirus. Dans le résultat ci-dessous, nous avons choisi des valeurs raisonnables pour ces paramètres.
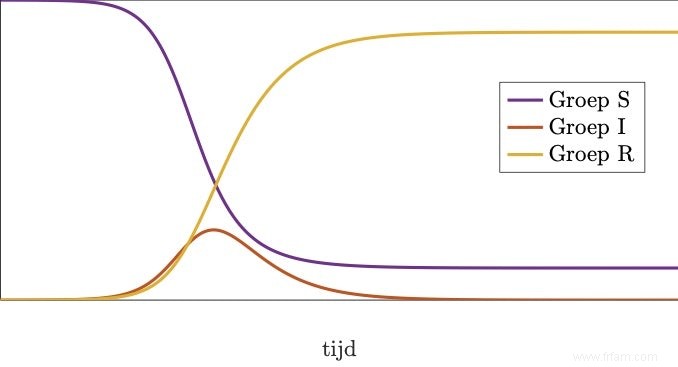
La courbe rouge ici donne $I$, et est exactement la même que la courbe rouge de la première figure. Il semble un peu plus petit car $S$ et $R$ sont désormais également sur le graphique. Expliquons maintenant le cours de $S$, $I$ et $R$ sur la base de la représentation schématique du modèle SIR. Du groupe S, il n'y a qu'une flèche qui éloigne points. Cela signifie que le nombre de personnes susceptibles de contracter la maladie ne peut que diminuer avec le temps. De l'autre côté du schéma on fait le même raisonnement :il n'y a qu'une flèche pointant vers points R, de sorte que le nombre d'individus immunisés continuera d'augmenter. Pour le groupe I, il y a à la fois une flèche entrante et une flèche sortante. Au début de l'épidémie, alors que peu de personnes sont encore infectées (le groupe I est petit) et que de nombreuses personnes sont sensibles (le groupe S est grand), la transition de S à I se fera beaucoup plus rapidement que de I à R. Dans d'autres mots, la flèche entrante bat la flèche sortante et le nombre de personnes dans le groupe I augmente. Au départ, cette augmentation se produit de plus en plus vite. C'est la phase de l'épidémie où il y a une croissance exponentielle du nombre d'infections. Au cours de cette phase, le groupe I grandit et le groupe S diminue. Au fil du temps, si peu de personnes sont susceptibles qu'il devient difficile pour le virus d'infecter de nouvelles personnes. Progressivement, la flèche sortante de I à R commence à battre la flèche entrante. Le nombre de personnes infectées diminue alors à nouveau. De cette façon, nous voyons la courbe corona émerger.
Étant donné que le paramètre $\beta$ modélise la facilité avec laquelle le virus se propage, c'est exactement le paramètre que nous pouvons influencer en tant que société. Dans nos simulations, nous considérons une population de 11 millions de personnes, soit environ le nombre de Belges. Nous supposons que les « mesures de confinement » seront mises en œuvre 100 jours après le début de la propagation de la maladie. Cela fait baisser la valeur de $\beta$ et la courbe montre une trajectoire différente et plus plate. Vous pouvez le voir dans l'animation ci-dessous.
Abaisser $\beta$ fait que le pic de la courbe reste beaucoup plus bas. La capacité des hôpitaux sera alors plus courte, moins forte ou, espérons-le, même pas dépassée. Les patients deviennent plus « étalés » avec le temps. Le pic ne se produit également que plus tard. Nous pouvons également vérifier l'impact du confinement sur le nombre de personnes sensibles, infectées et immunisées. En utilisant un modèle légèrement modifié, nous pouvons encore diviser le groupe R en personnes décédées et guéries. De cette manière, nous obtenons l'animation ci-dessous, dans laquelle, pour différentes valeurs de $\beta$, le nombre de personnes guéries, susceptibles, infectées et décédées est affiché pendant 1 an.
Notez que plus nous pouvons réduire $\beta$ en respectant strictement les consignes de confinement, moins il y aura de personnes infectées par le virus et plus le nombre de décès attendus sera faible. Nous concluons :"restez dans votre chambre" !
Ceux qui souhaitent plus de détails peuvent trouver notre article un peu plus détaillé en anglais ici.