Comment une maladie infectieuse comme Ebola se propage-t-elle dans une population ? Philippe Beutels et Niel Hens font des modèles mathématiques des maladies infectieuses et aident ainsi les autorités compétentes à faire les bonnes estimations.
Comment une maladie infectieuse telle qu'Ebola se propage-t-elle dans une population ? Et comment maîtriser la maladie le plus rapidement possible ? Philippe Beutels et Niel Hens élaborent des modèles mathématiques de maladies infectieuses et aident ainsi les autorités compétentes à faire les bonnes estimations.
Je regarde non seulement si des interventions, telles que l'utilisation de vaccins ou la fermeture d'écoles, ont du sens, mais aussi combien elles coûtent et ce qu'elles rapportent exactement », explique Philippe Beutels. Au Centre d'économie de la santé et de modélisation des maladies infectieuses, il étudie comment les maladies infectieuses, telles que la grippe ou la rougeole, se propagent dans une population et quelles mesures peuvent garantir que la maladie est contrôlée, voire éradiquée.
Ces dernières années, Beutels a été interrogé par le ministère de la Santé sur l'opportunité de vacciner tous les enfants en Belgique contre l'hépatite A, la varicelle, les pneumocoques, le rotavirus et la grippe. Puis son centre a fait à chaque fois un modèle mathématique différent, il a collecté des analyses d'échantillons de sang ou de salive en étroite collaboration avec des médecins, et ils ont étudié les options de vaccination. Et si tous les enfants recevaient un vaccin ? Ou tous les professionnels de santé, ou tous les voyageurs ? Il a ensuite formulé des recommandations basées sur les résultats. «Dans le cas de l'hépatite A, il s'est avéré qu'il était inutile de vacciner toute une cohorte de naissance d'enfants, car cela n'était en aucun cas rentable», dit-il, «alors que pour d'autres vaccins, il s'est souvent avéré être rentable.'
Étant donné que la simulation de maladies infectieuses au niveau d'une population implique beaucoup de mathématiques pures et d'informatique et que Beutels souhaitait toujours améliorer les modèles qu'il utilisait, il a commencé à chercher des groupes de mathématiques avec lesquels travailler. Après plusieurs collaborations sporadiques, il rencontre Niel Hens. Il venait de terminer une thèse en statistique. "L'un des sujets abordés était la modélisation précise du risque d'infection avec des données incomplètes", déclare Hens.
Statistiques
Les deux hommes ont tellement bien cliqué qu'ils ont continué à travailler ensemble. "Notre portefeuille de recherche s'est considérablement élargi depuis notre première réunion", déclare Beutels. « Nous ne modélisons plus seulement la transmission directe des infections entre les personnes via l'air, la salive, le sang ou le sexe, mais aussi indirectement via les moustiques ou d'autres animaux. En Belgique et dans d'autres pays. Cela n'aurait jamais été possible sans cette collaboration intensive.
Comment une épidémie de rougeole est-elle possible dans un pays où la maladie a été éradiquée par la vaccination ?
Leur collaboration consiste principalement à pousser le plus loin possible les méthodes mathématiques et statistiques dans la modélisation de la propagation d'une maladie. "Si nous prenons l'exemple d'Ebola, nous recherchons un modèle mathématique qui décrit le mieux les données que nous observons et nous examinons ce que cela signifie pour l'avenir", explique Hens. « Qu'est-ce que cela signifie pour estimer le nombre de cas d'Ebola et que pouvons-nous apprendre des différences entre les régions pour contenir Ebola tant qu'il n'y a pas encore de vaccin ? Et si un vaccin devient disponible, comment et où peut-il être utilisé au mieux ? Parce qu'au début il n'y aura pas assez de vaccins pour tout le monde."
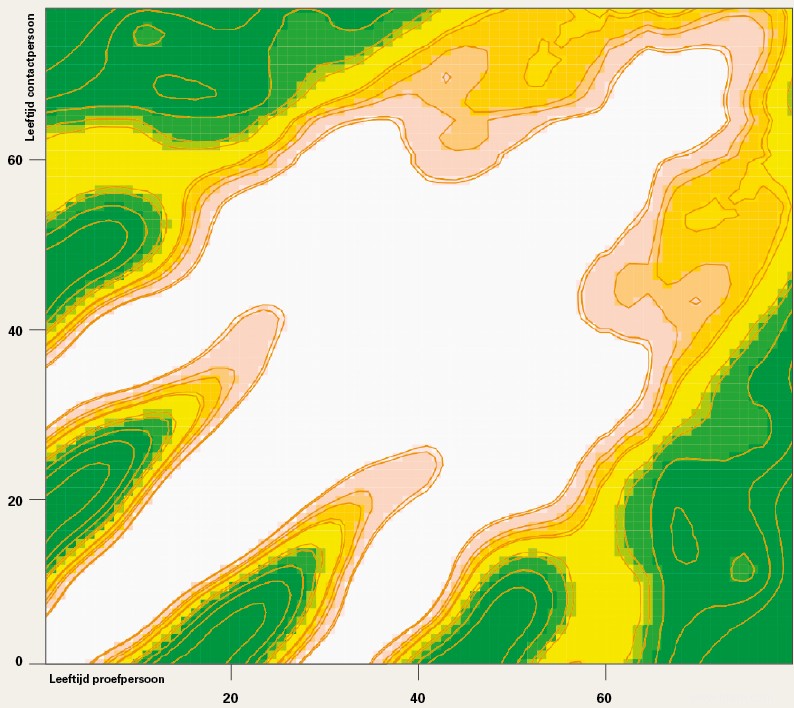
Les contacts sociaux entre les personnes sont souvent le moteur de la propagation des infections. «Nous semblons généralement fréquenter des personnes de notre âge, mais il existe également de nombreux contacts entre les parents et leurs enfants et entre les grands-parents et leurs petits-enfants», explique Hens. "Il est également intéressant de prendre en compte les types de contacts qui sont importants pour la propagation de la maladie :les contacts où les gens se serrent souvent la main ou les contacts où ils passent beaucoup de temps dans la même pièce."
Épidémies locales
Le fait que les modèles ne soient pas purement théoriques a été prouvé lors des épidémies d'oreillons et de rougeole ces dernières années. Ils ont suivi les schémas d'âge prédits par Hens et Beutels. Cependant, ces maladies ont progressivement disparu après le début de la vaccination systématique dans les années 1980. "Parce que la campagne de vaccination n'a pas pu atteindre tout le monde à l'époque, certaines personnes dans notre pays sont encore sensibles à la rougeole", explique Hens. « Donc, si une personne atteinte de rougeole entre dans notre pays et entre en contact avec des personnes sensibles, il pourrait y avoir une épidémie locale de rougeole. Nous pouvons estimer, sur la base de données spécifiques à l'emplacement, qui est le mieux vacciné et où.'
Beutels et Hens n'ont jamais connu le fait que la collaboration entre différentes disciplines est souvent difficile. « En raison de nos parcours différents, nous ne nous comprenons pas toujours tout de suite », admet Hens, « mais c'est ce qui le rend intéressant. Parfois, lors de la résolution d'un problème épidémiologique, un problème statistique se pose. Ensuite, je l'examine d'abord avec mes collègues et ensuite j'essaie d'expliquer à Philippe comment nous devrions résoudre ce problème. De cette façon, nous pouvons rapidement reconnaître ces problèmes s'ils se reproduisent.'
Beutels et Hens espèrent développer à terme des modèles tenant davantage compte des différences entre les individus. «Nous travaillons déjà sur des modèles basés sur l'individu dans lesquels nous modélisons réellement une population comme une collection d'individus séparés avec un certain nombre de caractéristiques, mais cela n'en est qu'à ses balbutiements», déclare Beutels. «À long terme, nous voulons inclure des informations génétiques, à la fois sur les individus et sur les agents pathogènes. Je pense qu'il y a de fortes chances que chaque bébé à l'avenir reçoive une puce contenant toutes ses données génétiques, sur la base desquelles nous pourrons améliorer encore ces modèles.'
Philippe Beutels est ingénieur commercial et docteur en sciences médicales. Il est professeur à l'Université d'Anvers, professeur invité à l'Université de New South Wales (Australie) et conseiller auprès de l'Organisation mondiale de la santé. À l'Université d'Anvers, il a fondé le Centre d'économie de la santé et de modélisation des maladies infectieuses. Il mène des recherches sur l'impact des interventions contre les maladies infectieuses, les déterminants de la consommation de drogues et le fondement socio-éthique de la priorisation des soins de santé.
Poules Niel a étudié les mathématiques à l'Université de Hasselt et à la KU Leuven. Depuis 2009, il est titulaire de la chaire de vaccinologie factuelle à l'Université d'Anvers et chargé de cours en biostatistique à l'Université de Hasselt. Il se spécialise dans l'utilisation et le développement de méthodes mathématiques et statistiques pour mieux comprendre la propagation des maladies infectieuses. Il est membre de la Young Academy depuis 2014.
