Il y a quelques années, je suis devenu fasciné par les propriétés électriques de l'eau. Eh bien, il y a un an, j'ai réalisé que je ne pouvais le comprendre qu'en comprenant les propriétés électriques de la glace (voir blog précédent). J'ai eu de la chance cependant, le travail dans la glace était déjà fait. Dans les années 1960, Jaccard a développé une théorie complète décrivant comment les charges se déplacent dans la glace. J'étais un peu surpris. J'ai étudié intensivement les solides pendant mes études. Pourtant, personne ne m'a alors expliqué à quel point les propriétés électriques de la glace sont particulières. Le solide le plus courant à la surface de la Terre est trop peu connu.
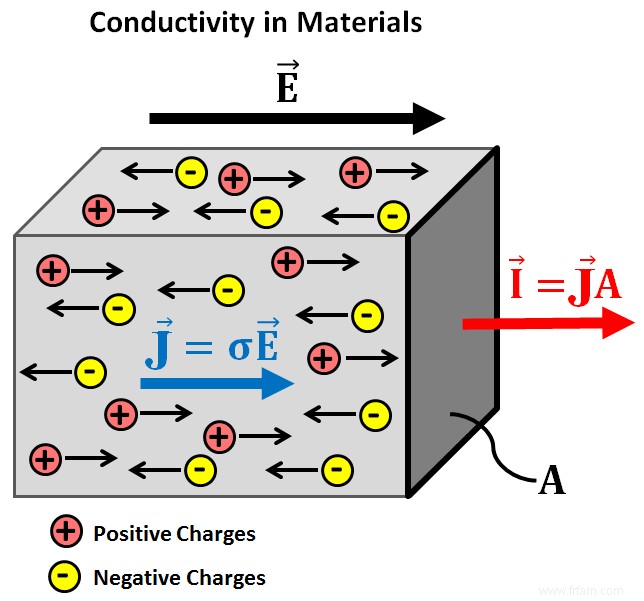
Jaccard s'est rendu compte que dans la glace il y avait un fort couplage entre l'orientation des molécules d'eau et le mouvement des porteurs de charge, ce qui est tout à fait exceptionnel. Dans presque tous les autres solides, les porteurs de charge (par exemple les électrons, les trous, les ions, ...) traversent la structure sans la modifier fondamentalement (voir Fig. 1). Ce n'est pas le cas dans la crème glacée et nous vous expliquerons en détail comment cela fonctionne dans un prochain blog. Cependant, le thème de ce blog est… les mathématiques.
Jaccard a réussi à résumer la relation entre l'orientation des molécules d'eau et le mouvement des charges dans la glace en quelques équations (voir Fig. 2). Ceux-ci sont également assez faciles à résoudre analytiquement. La théorie de Jaccard était née et l'accord avec les résultats expérimentaux était impressionnant.
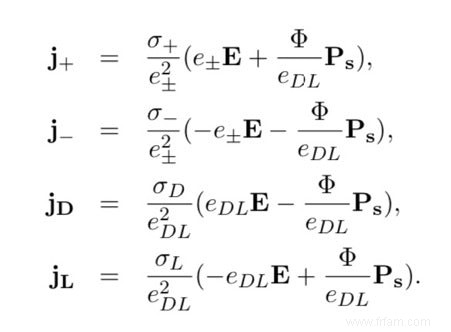
Une fois que les physiciens ont un ensemble cohérent d'équations, ils se calment et sentent qu'ils comprennent parfaitement le système. Mais est-ce vraiment le cas ? Bien sûr, les comparaisons de Jaccard ne sont pas sorties de nulle part. Ils ont été construits étape par étape à partir des équations de Maxwell et de certaines hypothèses sur la structure de la glace. La véritable perspicacité n'est pas dans les formules, mais dans la façon dont ils sont arrivés à ces formules. Et ici le bât blesse. Dans sa première dérivation, Jaccard a utilisé des arguments cinétiques évidents pour décrire le mouvement des porteurs de charge dans la glace. Mais il est toujours ressorti un facteur 2 de trop dans les seconds termes de la Fig. 2 (donc il y avait 2 Phi au lieu de Phi). Il n'y arrivait pas et après plusieurs années de recherche, il força le propos :il remplaça sa dérivation cinétique initiale par une dérivation beaucoup plus abstraite (à partir de certaines propriétés thermodynamiques générales de la glace) qui donna le bon résultat. Cependant, la nouvelle approche n'expliquait pas pourquoi l'approche cinématique ne fonctionnait pas. Un problème fondamental était clairement caché ici.
Les formules de Jaccard ont rapidement connu le succès et ont permis une compréhension approfondie de plusieurs résultats expérimentaux. Qu'ils ne soient pas si faciles à distraire fut vite oublié. Mais le problème ne m'a pas lâché. Je voulais appliquer ces équations dans le contexte de l'eau, donc je devais comprendre exactement comment elles étaient construites. Sinon, comment pourrais-je étendre les formules à la structure de glace interstitielle de l'eau (voir blog précédent). J'ai donc recommencé la distraction sur laquelle Jaccard s'était coincé.
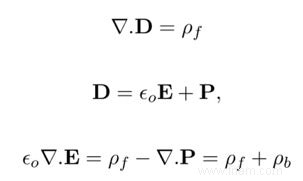
je suis prof. Pauwels (mon professeur à l'Université de Gand) est toujours reconnaissant de m'avoir donné un aperçu approfondi de la théorie de l'électromagnétisme. Je me suis vite rendu compte que le facteur 2 n'était pas le seul maillon faible de la théorie de Jaccard. La distinction entre les frais gratuits et liés était également assez négligente (pour les scientifiques parmi vous, voir la figure 3). En incluant systématiquement cette distinction, j'ai pu construire la théorie d'une manière beaucoup plus simple et corriger certaines erreurs (comme ce facteur de 2) (la description complète peut être trouvée ici).
Les équations pourraient donc être dérivées de considérations cinétiques évidentes. Ce détour thermodynamique était inutile. Je pouvais maintenant mieux visualiser le fonctionnement réel du mouvement des porteurs de charge (voir le prochain blog) et rendre les mathématiques derrière ces processus plus accessibles. De ce fait, j'étais vraiment prêt à étendre la théorie de Jaccard à l'eau.

Je voulais juste partager cette histoire. Non seulement parce que c'était mon premier véritable succès dans une recherche de plusieurs années, mais aussi parce que cela en dit long sur ce qu'est une véritable perspicacité (ou « compréhension approfondie »). Je le vois souvent avec mes élèves. Ils pensent qu'ils comprennent quelque chose parce qu'ils peuvent écrire la formule correcte, mais ils n'ont pas une image claire de l'histoire derrière ces formules. Quelles sont les conditions? Que signifie à nouveau chaque grandeur ? Quelle est l'influence de ce facteur quadratique ?... Certains manuels de physique et de nombreux articles en ont assez du même lit. Les comparaisons volent autour de vous sans prêter suffisamment attention à leur signification. Les dérivations mathématiques difficiles sont devenues un symbole de statut social, quelque chose comme "Regardez comme je suis intelligent." Mais la véritable perspicacité n'est-elle pas cachée dans les dérivations simples ? Difficile est alors synonyme de :« Je ne comprends pas encore tout à fait ».
Cela ne veut pas dire que la physique n'a pas besoin de formules. "Le livre de la nature est écrit dans le langage des mathématiques", a déclaré Galilée à juste titre, mais en même temps, il était aussi l'homme qui a pu expliquer ses connaissances mathématiques à un large public à travers des dialogues fascinants (Fig. 5).
Maintenant que l'histoire derrière les formules de Jaccard est claire, nous pouvons commencer le vrai travail dans le prochain blog (Pourquoi la glace est-elle un semi-conducteur spécial ?). Qu'en est-il de la conductivité électrique dans la glace et qu'est-ce qui la rend si spéciale ? Ce sera un blog pour les fonceurs, ceux qui veulent vraiment approfondir et enrichir leur compréhension du sujet. Je vous promets que je n'utiliserai pas de formules mathématiques.