Au cours d'un trajet sans fin, vous regarderez sans aucun doute l'écran du GPS pour voir combien de temps il roule encore. Le fait que l'appareil puisse vous dire cela est grâce à une technologie intelligente dans laquelle beaucoup de mathématiques sont réunies. La mathématicienne Ann Dooms (VUB) explique le fonctionnement de cette technologie.
Le GPS de votre voiture ou de votre smartphone peut être localisé n'importe où dans le monde, grâce à 24 satellites qui planent à 20 000 kilomètres au-dessus de nos têtes et orbitent autour de la terre en 12 heures.
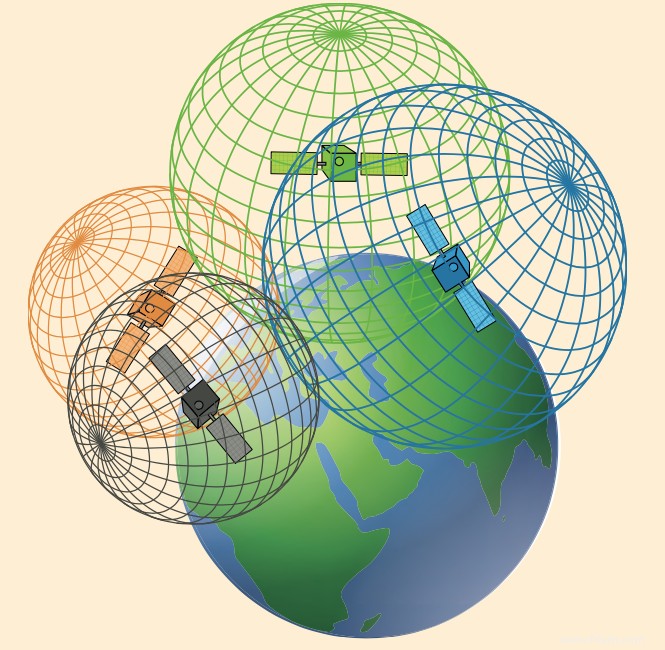
Parce qu'un satellite envoie un signal radio à votre appareil, il peut déterminer la distance à ce satellite. Cela signifie que vous êtes dans la voiture quelque part dans une sphère sphérique autour du satellite. Un satellite ne suffit pas pour calibrer votre position exacte. Votre distance par rapport à un deuxième satellite limite vos positions possibles d'une sphère à un cercle (l'intersection des deux sphères des satellites). Un troisième réduit encore plus votre position à seulement deux emplacements possibles. Avec un quatrième, votre position est déterminée de manière unique. Il peut maintenant être donné en coordonnées exprimées en latitude et longitude. Lorsque vous vous déplacez, votre position sera constamment redéfinie. Ce processus est connu sous le nom de trilatération.
À partir de ces données, Google Maps, Waze et d'autres programmes de navigation peuvent extraire toutes sortes d'informations sur votre itinéraire, telles que les routes à suivre et votre heure d'arrivée estimée. Les programmes utilisent une carte montrant toutes les routes du monde, complétées par leurs coordonnées et longueurs correspondantes. Pour chaque rue, le logiciel connaît la limitation de vitesse. Mais pour le calcul de l'heure d'arrivée, elle doit aussi tenir compte du trafic sur la route. C'est pourquoi elle garde également une trace de la vitesse à laquelle les conducteurs du passé ont conduit sur une certaine route et à quelle heure de la journée ils l'ont fait.
Toutes ces données sont collectées sur un graphique, une représentation des données avec leurs relations mutuelles. Il montre les villes et les intersections, même les maisons et comment elles sont reliées par des routes. Des informations supplémentaires sur le temps et la longueur sont ensuite ajoutées aux connexions sous forme de "poids" - nous parlons d'un graphique pondéré.
Lorsque vous entrez une nouvelle destination, vous pouvez choisir l'itinéraire le plus rapide ou le plus court. Le programme calcule ensuite quel itinéraire répond à cette exigence. Pour cela, il utilise un algorithme développé par Edsger Dijkstra (1930-2002) en 1956. Il vous donne une recette étape par étape sur la meilleure façon de parcourir le graphique, de sorte que vous obteniez une liste des routes de votre départ à votre destination finale qui, ensemble, forment la ont le moins de poids en termes de temps ou de distance.
La théorie des graphes est née d'un problème d'itinéraire concret. En 1736, le mathématicien Leonhard Euler (17071783) a étudié une question de certains habitants de Königsberg (aujourd'hui Kaliningrad en Russie) en Allemagne. La rivière Pregel a divisé la ville en quatre parties, dont deux sont des îles. Ces parties étaient reliées par un total de sept ponts. Les habitants voulaient pouvoir traverser la ville à pied et traverser chaque pont exactement une fois, puis rentrer chez eux.
Euler a fait une représentation abstraite de la ville. En fin de compte, peu importe où se trouvent les ponts, il s'agit de savoir quelles parties de la ville ces ponts relient. Ainsi est née la théorie des graphes. Il a prouvé que le voyage demandé est impossible. Pour cela, vous devez avoir un nombre pair de ponts de connexion. En effet, à chaque fois que vous arrivez dans un quartier, vous devriez pouvoir repartir avec un pont inutilisé. Dans les cas où une telle marche est possible, on parle de cycle d'Euler. Peut-être que Google peut intégrer l'option de cycle Euler en tant que fonctionnalité supplémentaire dans Maps. Peut être utile, maintenant que nous avons tous redécouvert la marche.