Le mathématicien Jacques Tits est décédé le 5 décembre à l'âge de 91 ans. Il était surtout connu pour la théorie des groupes, pour laquelle il a reçu le prix Abel.
Le mathématicien Dirk Huylebrouck a écrit cet article à l'occasion de la cérémonie de remise des prix, paru dans le magazine Eos en 2008.
Les mathématiciens du siècle dernier avaient un problème mondain :Alfred Nobel pensait qu'ils n'étaient pas assez appliqués pour le « bien de l'humanité » et n'avait donc pas prévu de prix. C'est pourquoi une médaille Fields a été créée plus tard, du nom du mathématicien canadien John Charles Fields. La médaille a longtemps été considérée comme un prix Nobel non officiel, mais elle n'est décernée que tous les quatre ans, et uniquement aux scientifiques de moins de 40 ans. Depuis 1978, le prix Wolf a parfois été considéré comme une meilleure alternative au vide noble, mais finalement les Scandinaves ont résolu le problème eux-mêmes en introduisant un prix Abel annuel d'une valeur de 750 000 euros.
Cela se passe depuis 2003, un an après la célébration du bicentenaire de la naissance du mathématicien norvégien Niels Hendrik Abel (1802-1829). Il faudra peut-être encore plusieurs années et des noms prestigieux pour être ajoutés à la liste des honneurs pour que le prix soit ancré dans l'esprit humain en tant que mathématicien prix Nobel. Abel-Nobel :ça rime déjà bien. Jacques Tits a reçu presque tous les prix en mathématiques, à l'exception de la médaille Field mentionnée, pour laquelle il s'est avéré être un peu trop vieux. Et pourtant, il avait commencé les maths assez tôt. Né le 12 août 1930, à Uccle (Bruxelles), afin de joindre les deux bouts après la mort de son père (également mathématicien) à l'âge de treize ans, il commence à donner des cours particuliers à des jeunes de quatre ans son aîné. Jacques a séché quelques années scolaires et à quatorze ans, il est premier au concours d'entrée d'ingénieur à l'Université Libre de Bruxelles (ULB). Cela lui permet d'entamer des études de mathématiques et d'obtenir son doctorat en mai 1950 à l'âge de dix-neuf ans. Il reste à l'ULB jusqu'en 1964, puis intègre l'Université de Bonn et enfin, en 1973, le Collège de France à Paris. Tits est devenu membre d'académies en France, aux États-Unis, en Belgique et aux Pays-Bas, et s'est vu offrir des diplômes honorifiques des universités d'Utrecht, Gand, Bonn et Louvain-la-Neuve. Et tout cela pour travailler en groupe et concevoir des bâtiments (voir encadré).
Tits formule dès 1974 sa thèse fondamentale sur la reconnaissance des groupes complexes via certains édifices, dans un livre volumineux avec tous les détails et élaborations. Que le jury du prix Abel, comme celui du prix Nobel de physique, ait également attendu des applications décisives des théories de Tits est douteux. En tout cas, ils existent entre-temps :il y a aussi des bâtiments qui ne sont pas tellement considérés comme des modèles de groupes et qui se sont pourtant révélés indispensables dans la géométrie moderne, et ont même des ramifications jusqu'à la théorie du codage.
Il arrive plus souvent en mathématiques qu'une invention devienne plus intéressante lorsqu'elle dépasse sa destination (ce qui est aussi le cas dans d'autres sciences, ou, en vérité, dans l'art). Tout comme certaines machines à laver portent aujourd'hui l'inscription logique floue se référant à une sorte de logique mathématique, il est concevable qu'une nouvelle étiquette apparaisse sur le lecteur de CD dans un proche avenir :Basé sur les bâtiments de Seins † En tout cas, Jacques Tits lui-même le sait mieux :"Ce ne sont pas les applications qui font la beauté des mathématiques, mais les mathématiques qui rendent les applications belles."
En Belgique, le nom de Jacques Tits est connu et aimé de ses nombreux "élèves", comme le Prof. Em. Francis Buekenhout (ULB), Bernhard Mühlherr (ULB), Jean-Pierre Tignol (Louvain-la-Neuve), Hendrik Van Maldeghem (UGent), et parmi les membres de leurs équipes de recherche. Ils sont particulièrement heureux de l'attribution du prix Abel à Jacques Tits, notamment parce qu'ils le connaissent comme un homme toujours sympathique, sans coupe de cheveux et avec un sens de l'humour. Quand la moitié des lumières s'est éteinte pendant un cours au Collège de France, il a plaisanté en disant que la moitié sombre du tableau serait réservée aux fautes. Et depuis Mésanges, de nombreux mathématiciens ont une préférence pour le même dessert :lors d'un dîner conférence, le lauréat du prix Abel a interrompu l'ambiance (trop) solennelle d'un grand cri :"Pour moi une mousse au chocolat !"
Tits a reçu le prix Abel pour "ses profondes réalisations en algèbre et en particulier pour sa mise en forme de la théorie moderne des groupes". Un « groupe » mathématique est une structure qui peut être très abstraite. Les entiers "ordinaires" 0, 1, -1, 2, -2... forment "un groupe mathématique", avec l'addition habituelle :autrement dit, une fois les règles de base du calcul connues, tous les calculs se font dans ce cadre.
Cependant, cela peut être encore plus abstrait. Considérons un triangle ABC et deux opérations :'a', la réflexion autour de la médiane passant par A, et 'b', la rotation de 120° dans le sens inverse des aiguilles d'une montre.
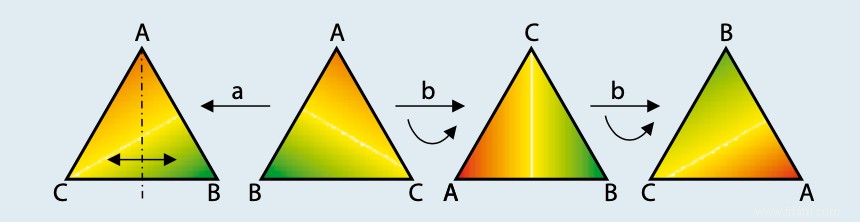
L'enchaînement de deux opérations s'appelle alors la 'composition', et il joue le rôle d'addition pour les nombres entiers. Avec l'opération 'n', 'ne rien faire', a et b forment alors un 'groupe'. Les maths ou le jeu peuvent commencer, bien que l'on remarque rapidement qu'un certain nombre de règles de 'calcul' sont différentes qu'avec les nombres entiers :par exemple, 'a na n'est rien d'autre que n, tout comme 'b na b na b'/ Cela peut être désigné par les notations usuelles des carrés et des cubes :'a na a' =aa =a =n; analogue :b=n. Cependant, 'a après b' n'est plus égal à 'b après a' (ab =(ab ≠ ba), alors qu'avec les entiers ordinaires '2+3 =3+2' s'applique bien sûr.

Certains voient cela rapidement, tout comme certains peuvent résoudre un Rubik's cube très rapidement (et c'est aussi la théorie des groupes). Les mathématiciens travaillent si souvent avec ces groupes que dans le cas de l'exemple, ils ne pensent plus à un triangle en rotation et en miroir, mais voient ce groupe d'opérations comme une abstraction de ce triangle équilatéral. C'est un peu comme quand on apprend à compter :au début on additionne 2 vaches et 3 vaches, mais petit à petit cela s'abstrait à 2 + 3. Un cristal n'est alors plus décrit par ses dimensions précises, mais par le ' groupe' qui lui est associé. Cette abstraction a un grand avantage, car de même qu'il n'est plus important de compter si les vaches ou les pommes sont additionnées, en théorie des groupes, peu importe que les calculs soient faits avec des triangles, des cristaux, des quantités physiques ou des règles de mariage.
Un exemple plus compliqué de groupe est produit par les opérations a et b vérifiant les relations suivantes :
n =a2 =b3 =(ab)13 =(a−1b−1ab)5 =(a−1b−1 a−1b−1abab)4 =(abababa-bab−1)6.
Le « n » représente à nouveau l'opération « ne rien faire », de sorte que les premières relations, a2 =n et b3 =n, rappellent les lois qui s'appliquent également lors de la mise en miroir et de la rotation d'un triangle. L'expression suivante avec la treizième puissance de ab, cependant, montre qu'il semble s'agir d'autre chose. Jacques Tits réussit à merveille à imaginer à quel point ce « groupe » peut compter, au point qu'on l'appelle même aujourd'hui le « groupe des Seins ».
La création la plus connue de Tits est sa « théorie de la construction », qui permet de comprendre les groupes abstraits. Le nom a été inspiré par la division supplémentaire de la structure en « appartements » et « chambres ». Une succession de pièces avec de nombreuses parties communes s'appelle alors une 'galerie', mais sinon toute référence à l'immobilier est purement fortuite. Jacques Tits y était arrivé grâce à l'étude des soi-disant «groupes de Lie», du nom de Sophus Lie, un autre célèbre mathématicien norvégien du XIXe siècle. Tits a noté que les groupes de Lie contiennent des sous-groupes avec de fortes propriétés, les soi-disant «polyèdres réguliers en dimension supérieure». Il a généralisé ce concept, et plus tard ses «polytopes généralisés» ont été renommés «bâtiments» et les cas particuliers «appartements».
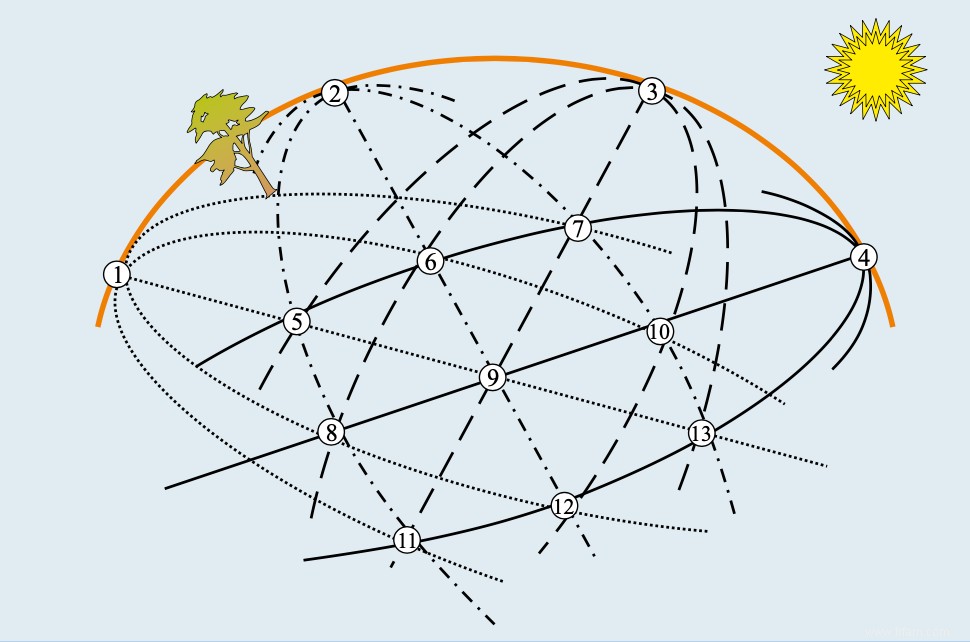
Un bâtiment Tits typique est beaucoup plus complexe, mais la définition formelle d'un bâtiment Tits embrasse des lois de base géométriquement similaires :deux pièces doivent toujours être dans un appartement, tandis que deux appartements doivent toujours avoir certaines parties en commun. Le grand mérite de Tits était d'avoir pu montrer que certains groupes de Lie complexes se reconnaissaient à la présence de certains types d'édifices. Son traitement du «groupe de mensonges E8» est connu sous le nom de «construction du carré magique», ce qui est important en physique car le groupe joue un rôle dans la «théorie du tout». Cette "théorie de l'unification", image onirique d'Albert Einstein, tente de "regrouper" les différentes théories de la physique, afin que le comportement des particules élémentaires, les forces fondamentales de la nature et les plus grandes galaxies rentrent dans un même modèle. Mais ce cube Rubik de l'univers n'a même pas encore résolu les seins.