Année après année
Pour les visages de singe
Un masque de singe.
Matsuo Basho
(1644-1694)
En dehors des motifs pandémiques, fermer les frontières nationales et opter pour un isolement total peut parfois être bénéfique pour un peuple.
Prenez le Japon par exemple. Elle a vécu volontairement isolée de l'ouest pendant la période dite d'Edo de 1603 à 1867, et a de ce fait connu des évolutions économiques, philosophiques et culturelles fascinantes. Une grande partie de l'individualité japonaise telle que nous la connaissons aujourd'hui est née ou s'est épanouie. On pense aux geishas ou aux haïkus, mais aussi (et surtout) aux sangakus.

Ces tablettes en bois colorées étaient accrochées dans les sanctuaires shinto ou les temples bouddhistes à l'époque d'Edo, probablement comme cadeaux aux dieux ou aux saints.
Avec peu ou pas de texte, les sangakus illustrent une propriété géométrique auto-inventée sur les triangles, les carrés, les ellipses et surtout les cercles. Dites-le vous-même, un cadeau ne pourrait pas être plus touchant et noble. Parce qu'un sangaku était également visible pour les autres visiteurs du temple, le fabricant visait généralement une géométrie esthétique et une complexité impressionnante. Donc une bataille YouTube avant la lettre. Le sangaku idéal est une alliance mystique entre son créateur artistique, pure propriété géométrique (dieu) et le spectateur interpellé.
De nombreux sangakus nous sont connus grâce au travail missionnaire du mathématicien japonais Hidetoshi Fukagawa en Amérique. Par exemple, lisez
H. Fukagawa, D. Pedoe, Problèmes de géométrie des temples japonais , 1989.
de H. Fukagawa, A. Rothman, Mathématiques sacrées :géométrie des temples japonais , 2008.
À partir de là, nous montrons ce cinq-cercles-sangaku :
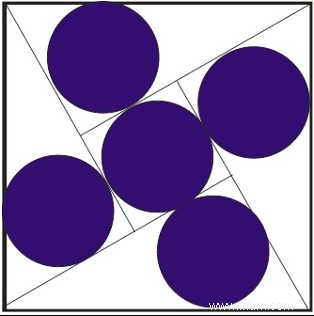
Si vous vous demandez comment ils ont réussi à serrer cinq disques circulaires identiques dans un carré de cette manière, nous pouvons vous rassurer. Cette question est exactement l'intention de ce sangaku. Un bon étudiant avec une formation géométrique peut calculer que la configuration ci-dessus ne réussit que si le rayon R des cercles est lié au côté Z du carré comme :
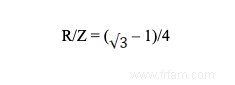
Même s'il faut dire que selon le cadre culturel ou le contexte du problème, ce n'est pas toujours la solution numérique qui est recherchée. Dans l'Antiquité grecque, par exemple, les problèmes géométriques étaient résolus avec de pures constructions de boussole et de règle, tandis qu'à l'époque d'Edo, la géométrie était parfois pratiquée à l'aide de l'origami. Essayez ce dernier par vous-même avec le défi (modeste) suivant. Placez un sous-bock rond (par exemple) dans le coin d'une nappe carrée ou d'un tapis en carton. Si nous plions le carré comme indiqué ci-dessous, jusqu'à ce qu'un côté touche le cercle, alors vous avez "déterminé" le rayon du cercle comme la longueur en saillie x .
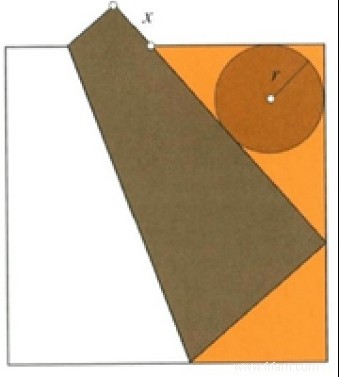
Comme beaucoup d'autres sangakus, le sangaku à cinq cercles est un exemple de pile mathématique † Les objets empilés peuvent être de n'importe quelle forme, taille ou dimension, tant qu'ils ne se chevauchent pas. Une belle illustration est l'empilement de 19 cercles identiques dans un triangle équilatéral imaginé par le mathématicien hongrois Farkas Bolyai.
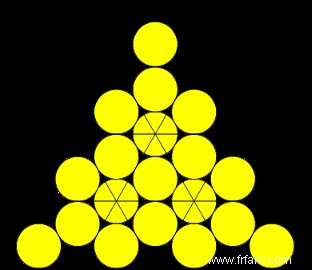
Il s'agissait d'un calendrier de plantation optimal pour les arbres. Nous voyons déjà des applications dans notre cave à vin. Il se trouve que les Hongrois sont très doués dans cette discipline. Zsófia Ruttkay cherche et s'inspire donc aussi de la nature pour des empilements de cercles « étroitement végétalisés », plus précisément dans l'expansion des nénuphars (dans le jardin de Monet, ou si l'on veut rester dans le thème, dans le bassin d'un temple bouddhiste) :

Au cours du XXe siècle, l'empilement est devenu une discipline mathématique à part entière. Dans le monde entier, il y a des gens qui remplissent professionnellement leurs journées réelles et leurs conteneurs imaginaires avec des cercles ou des sphères ou tout ce qui croise leur chemin. Habituellement, le défi de ces remplisseurs d'étagères de mathématiques maximiser la densité de la pile, ou en d'autres termes, minimiser l'espace perdu (vide). L'expertise d'un expert en géométrie dans l'empilement de cercles peut parfois s'avérer utile. Il sait combien de bouteilles de vin entrent dans une boîte et il sait comment découper autant de cartes de bière rondes que possible dans une feuille rectangulaire. De plus, au cas où il aime utiliser des mots difficiles, il sait où placer les points de constellation pour une modulation d'amplitude en quadrature optimale.
Mais un emballeur de cercle mathématique sait aussi combien de places vous pouvez installer dans un auditorium ou une salle de théâtre (et comment), avec la garantie d'une distance minimale entre les spectateurs. Ceci est précisé ci-dessous. Quiconque a maîtrisé l'art d'empiler de manière optimale 5 cercles dans un carré (bleu) sait également où placer cinq personnes dans un carré (rouge) afin que la distance au voisin le plus proche soit la plus grande possible. Et c'est exactement comme indiqué ci-dessous :
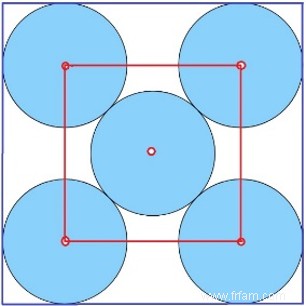
(Nous vous prions de nous excuser pour l'idée erronée répandue dans le monde universitaire consistant à confondre les gens avec des points infinitésimaux.)
Ci-dessous, vous pouvez voir comment notre empileur de cercles professionnel découpe N cercles à partir d'un carré de papier (bleu) afin de perdre le moins d'espace possible entre les deux. Ou comment il place N points personnes dans une pièce carrée (rouge) pour maximiser la plus petite distance entre deux personnes.

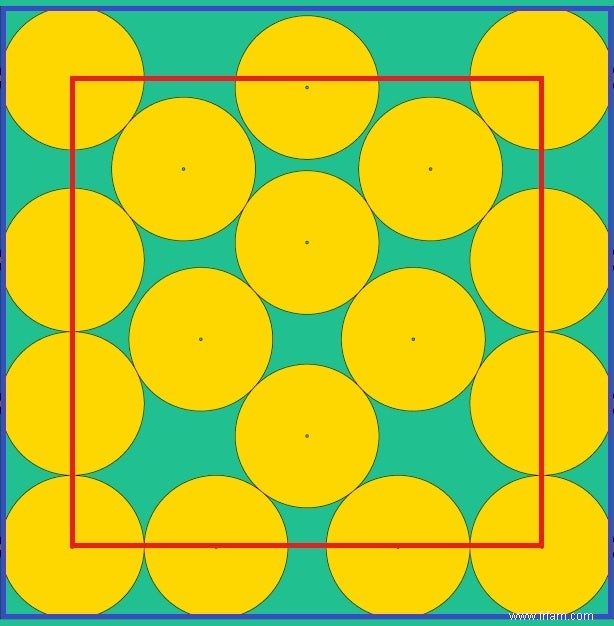
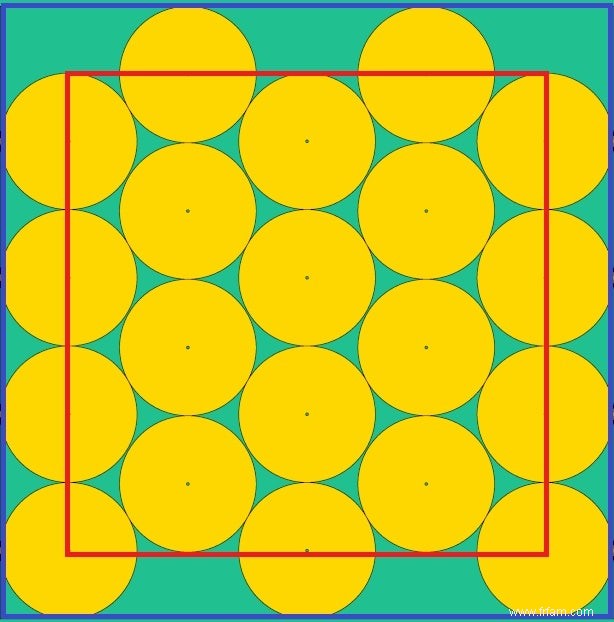
Ces exemples suggèrent que les modèles de cercles optimaux ne peuvent pas être déterminés par une formule fixe. En fait, le motif aux vingt cercles est le moins surprenant, car c'est la solution que tout collectionneur de vins ou transporteur de boîtes de soupe a déjà imaginée. C'est la disposition hexagonale bien connue , où chaque cercle toucherait exactement six autres si le contenant s'étendait à l'infini dans toutes les directions. D'après le Théorème de Thue (1890) ce motif hexagonal donne l'empilement optimal de cercles identiques dans un plan non borné, avec une densité maximale d'environ 91 % (π/  pour être exact) est atteint.
pour être exact) est atteint.

Dans tous les cas, cela nous humilie de noter que les abeilles n'ont pas besoin de mathématiques pour sécher leurs gouttes de miel dans ce modèle optimal d'hexagones réguliers.
Chaque nombre différent de cercles semble nécessiter une solution ad hoc, mais cela implique vraiment une certaine compétence mathématique. Et, bien sûr, le temps de calcul informatique. D'autre part, les mathématiciens de l'origami (oui, il y en a) comme Erik Demaine et Robert Lang ont montré qu'on ne trouvera jamais d'algorithme efficace pour calculer un empilement optimal de cercles pour une feuille de papier rectangulaire, ce qu'ils regrettent car cela aurait été utile lors du dessin de certains patrons de pliage.
Chaque nombre différent de cercles semble nécessiter une solution ad hoc, mais cela implique vraiment une certaine compétence mathématique. Et, bien sûr, le temps de calcul informatique. D'autre part, les mathématiciens de l'origami (oui, il y en a) comme Erik Demaine et Robert Lang ont montré qu'on ne trouvera jamais d'algorithme efficace pour calculer un empilement optimal de cercles pour une feuille de papier rectangulaire, ce qu'ils regrettent car cela aurait été utile lors du dessin de certains patrons de pliage.
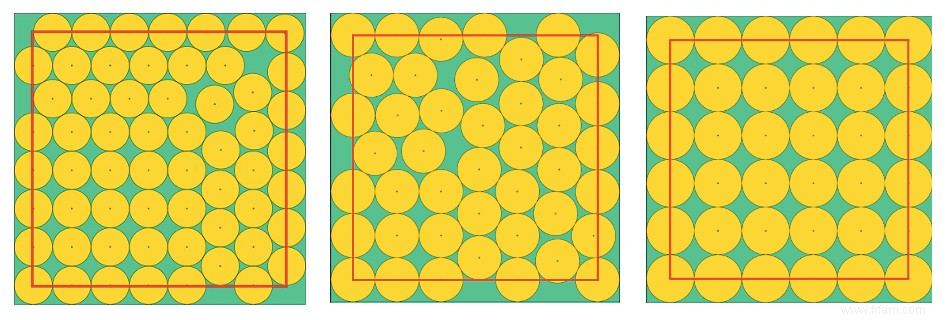
En guise de petit rappel ou de service pour les organisateurs parmi vous, nous avons calculé combien de spectateurs nous pouvons placer en toute sécurité lors d'une cérémonie ou d'un acte de scène dans un espace de dix mètres sur dix, indiqué ci-dessous par un carré rouge. Dans la première solution on peut mettre 59 chaises, en autant de centres de cercles pour lesquels on a pris un diamètre de 1,5 m. Ensuite la deuxième solution avec 43 chaises et un diamètre de 1,8 m est plus réaliste (30 cm de largeur aux épaules). Si vous préférez une marge encore plus grande, nous pouvons recommander des cercles d'un diamètre de deux mètres, pour lesquels l'ordinateur propose de manière inattendue une grille carrée de 36 points comme solution. Cela ne doit pas s'améliorer pour nous.
