Grâce au travail d'un mathématicien de 37 ans, on connaît enfin depuis l'été dernier la liste complète des pentagones convexes pour les revêtements de sol à 1 tuile, dernier obstacle pour connaître tous les polygones convexes pour les motifs à 1 tuile.
L'été 2017 a marqué une étape importante pour les décorateurs d'intérieur, les carreleurs, les coupeurs de carreaux et les bricoleurs créatifs. Le mathématicien Michaël Rao (École Normale Supérieure de Lyon) a prouvé à l'aide de son ordinateur un résultat qui répond à une question posée dans la Grèce antique ou même antérieure :
Quels polygones (convexes) peuvent former une tuile qui recouvre bien le visage (pas d'espaces ouverts, pas de chevauchements à moins de sommets ou de côtés entiers) ?
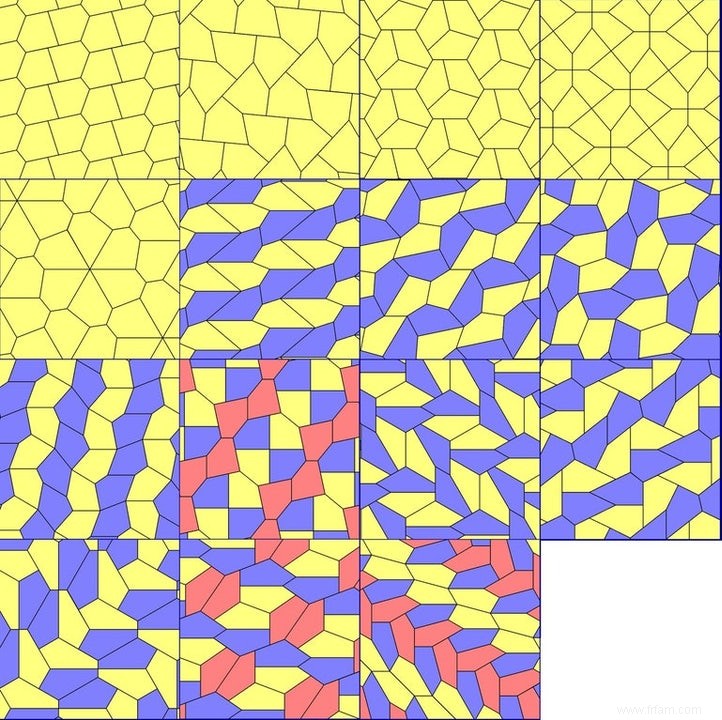
Depuis cet été, nous savons qu'il n'y a que 15 formes pentagonales convexes pour un motif à 1 tuile pour couvrir une surface plane. Consultez la liste complète ci-dessous :
Le résultat de Rao concerne les pavages monohédriques , où il n'y a qu'une seule forme de tuile (ou prototile ) peut être utilisé. De plus, il se limite à convexe pentagones, ce qui signifie que les diagonales sont toujours à l'intérieur du polygone.

Si vous souhaitez carreler le visage avec un seul prototile qui a la forme d'un polygone régulier alors les anciens Grecs savaient déjà que vous n'aviez le choix qu'entre 3 options :



Notez que la liste ci-dessus avec les 15 pentagones convexes pour un pavage monoédrique ne contient pas de pentagone régulier, car cela ne fonctionne pas. On sait depuis longtemps que tout triangle ou quadrilatère (même non convexe) peut paver le plan en un seul prototile. Les hexagones convexes pavant le monoèdre plan sont connus depuis 1918 :Karl Reinhardt a prouvé dans sa thèse qu'il n'existe que trois prototiles hexagonaux convexes possibles (dont l'hexagone régulier). Les 5 premiers de la liste complète des prototiles pentagonaux convexes ont également été décrits par Karl Reinhardt. Petit à petit, cette liste de pentagones s'est enrichie, avec la découverte du quinzième carreau tout récemment en 2015 par Casey Mann † Depuis l'été dernier, il est devenu clair que nous n'avons plus besoin de chercher des pentagones convexes qui recouvrent la surface à eux seuls. Selon ses propres mots, Mann était également proche de la preuve avec son ordinateur, mais il a été frappé sur la ligne par Rao (pas encore publié, mais déjà largement vérifié). De plus, il est prouvé depuis longtemps qu'un polygone convexe pavage du plan peut avoir au plus six sommets. Grâce au résultat de Rao, nous connaissons maintenant tous les polygones convexes pouvant être utilisés pour un pavage monoédrique.
Nous avons peut-être coché cette recherche, mais l'histoire du carrelage est loin d'être complète. Il reste beaucoup à dire sur les tuiles non convexes. L'analyse mathématique réalisable est généralement limitée aux tuiles polygonales, mais à partir d'un travail graphique tel que celui de M.C. Escher, nous apprenons que la forme des tuiles peut être très compliquée, même si vous n'utilisez qu'une seule forme de tuile :

L'étude des pavages devient également plus intéressante (et belle) lorsque nous utilisons plusieurs prototiles dans notre schéma de pose. On en trouve de beaux exemples dans les décorations arabes de l'Alhambra de Grenade :

Johannes Kepler (1571 – 1630) fut peut-être le premier à étudier systématiquement les modèles multi-prototypes :

En 1987, Grünbaum et Shephard ont publié leur manuel désormais légendaire, qui a définitivement mis ce sujet sur la carte en tant que sous-discipline des mathématiques.

Pour la commodité du carreleur, nous choisissons presque exclusivement un schéma de pose périodique pour les prototiles donnés. Cela signifie que le motif se répète à la fois dans un mouvement latéral et dans un mouvement ascendant. Vous pouvez clairement remarquer la répétition périodique dans les directions horizontales et verticales dans les motifs monohédriques grecs avec des polygones réguliers, mais aussi dans le motif de Kepler ou le travail d'Escher ci-dessus. Dans un pavage périodique, les deux directions dans lesquelles le motif se répète ne doivent pas nécessairement être perpendiculaires l'une à l'autre :

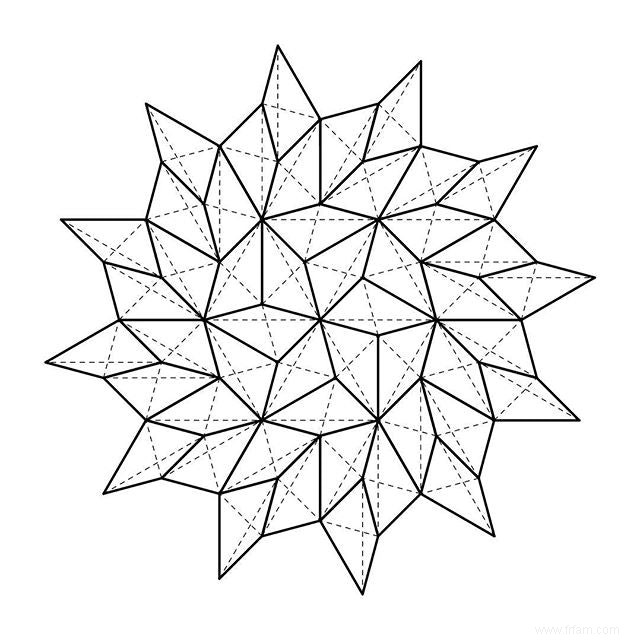
Cependant, ce motif non périodique est un fantasme volontaire du carreleur, car avec ce carreau, vous pouvez également opter pour un motif plus facile. Pendant longtemps, les mathématiciens ont pensé que tout ensemble fini de prototiles avec lequel paver le plan permettait également un motif périodique. Jusqu'à Robert Berger en 1964 une collection de prototypes d'une période trouvées pour lesquelles aucun schéma de ponte périodique n'existait. Cependant, ce premier contre-exemple se composait de 20426 prototiles, mais dans les années suivantes, d'autres ensembles apériodiques avec de moins en moins de prototiles ont été trouvés. L'exemple le plus célèbre est peut-être la découverte de Penrose (1973) consistant en seulement 2 formes de tuiles, un losange et un parallélogramme, qui peuvent paver le plan, mais jamais d'une manière où des répétitions périodiques se produisent dans une zone illimitée.

Onze ans après sa découverte, alors que les microscopes électroniques étaient suffisamment développés, ce même motif de Penrose a été reconnu dans la pseudo-symétrie d'un quasi-cristal :

Le Saint Graal pour les scientifiques de tuiles en ce moment est la quête d'un seul prototype apériodique, la quête d'ein-stein , une forme de tuile qui peut recouvrir la surface, mais jamais avec un motif périodique. Pour le moment, il n'est même pas clair si une telle tuile existe, mais les initiés le pensent (si cela vaut quelque chose). Attention, dans cette quête ein-stein, nous recherchons une tuile normale qui se compose de 1 pièce (cohérente ), car en 2010, Socolar et Taylor avaient déjà trouvé un prototile apériodique composé de plusieurs morceaux :
En tout cas, depuis l'actualité mondiale de l'été dernier, on sait que le prototile apériodique tant convoité ne peut pas être convexe. Ainsi, le résultat de Michaël Rao, 37 ans, garantit que nous avons maintenant un aperçu complet de tous les prototiles polygonaux convexes monoédriques, et ils semblent tous avoir un schéma de pose périodique. Ainsi, les chevaliers ein-stein ne peuvent désormais se jeter que sur des polygones concaves.