En effet, nous voyons le Tour de France 2019 comme une occasion de parler de mathématiques.
- Une contribution invitée du collègue Stijn Dierckx -
Vous ne pouviez pas le manquer début juillet :le 106e Tour de France a atterri au cœur de Bruxelles pour le Grand Départ , 50 ans après la première victoire d'Eddy Merckx sur le circuit. La première étape a commencé à Bruxelles pour faire une boucle via le Muur van Geraardsbergen en passant par Charleroi et revenir à Bruxelles. Rien d'étrange, à première vue. Mais le téléspectateur attentif du programme-cadre Vive le Vélo a déjà entendu Karl Vannieuwkerke le dire au lendemain de cette étape :« Si vous regardez cette étape sur la carte, vous arrivez presque à la forme de notre pays. Regardez ces contours, ça ressemble à la Belgique, est-ce que ça pourrait être une coïncidence, ou un film du chef de piste ?" Il ne faut pas répondre à cette question, mais force est de constater que la ressemblance est un peu frappante. Jugez plutôt :
Les cyclistes n'y ont probablement pas prêté trop d'attention ce jour-là, mais les mathématiciens sont (comme dans tant de domaines) différents. C'était un fait divers amusant sonne une cloche (de bicyclette), à savoir celle du théorème du point fixe de Brouwer. Ce théorème, que nous vous présentons un peu plus loin, a des applications en mathématiques, en physique, en logique, mais aussi en biologie et en économie. En effet, le théorème du point fixe était essentiel en économie pour prouver l'existence d'équilibres de marché (? Je ne suis pas économiste). Kenneth Arrow et Gérard Debreu ont reçu le prix Nobel d'économie en 1983. Il a également été utilisé dans la preuve originale de l'existence des équilibres de Nash, pour laquelle John Forbes Nash Jr. (l'homme du film A Beautiful Mind) a reçu le prix Nobel d'économie. Mais que dit exactement cette déclaration ? Dans sa forme la plus simple (?) :
Théorème
Une fonction continue d'un sous-ensemble convexe et compact d'un espace euclidien vers lui-même a au moins un point fixe, c'est-à-dire un point qui est mappé sur lui-même.
Pas très éclairant à moins que vous, en tant que lecteur, ne soyez compétent en topologie algébrique ou sur des questions connexes. En d'autres termes, une explication plus simple est plus que appropriée.
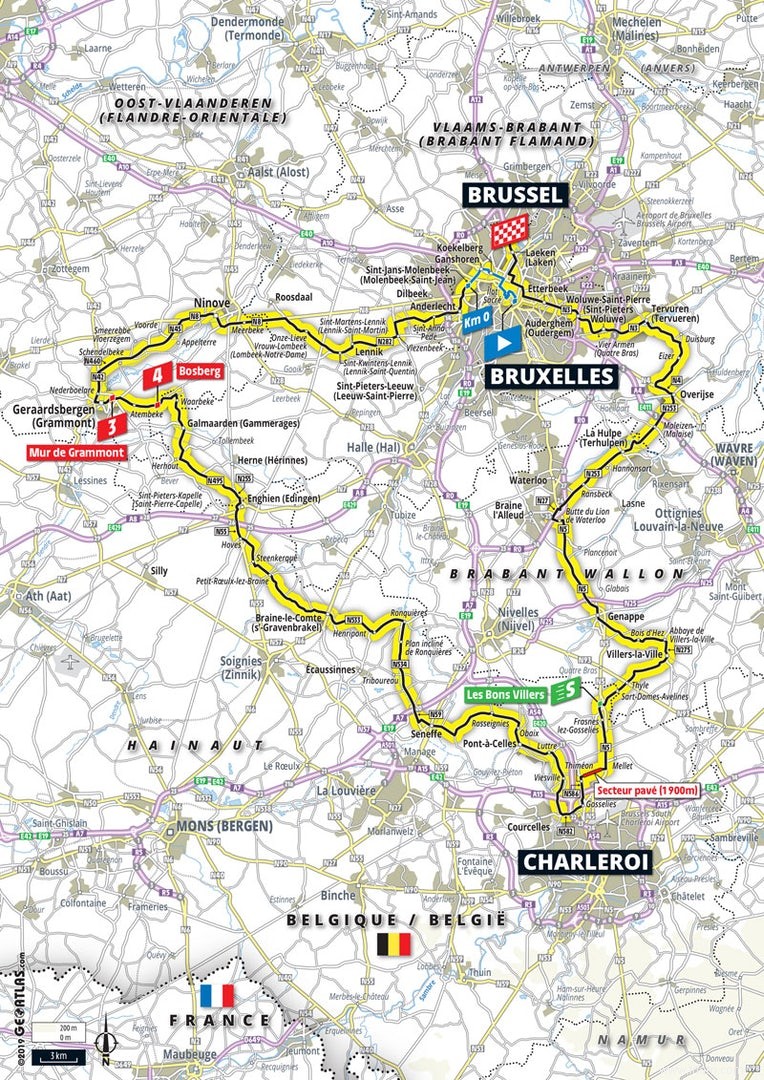
Nous considérons le cas le plus simple, à savoir une fonction continue $f$ de l'intervalle fermé $[0,1]$ en lui-même. Ce sont des fonctions que l'on imagine facilement à l'aide d'un graphe comme on nous le demandait trop souvent au lycée. Deux exemples de telles fonctions continues de $[0,1]$ à lui-même sont présentés ci-dessous :

En substance, c'est de cela qu'il s'agit. En partant d'un carré, tracez une ligne lisse (courbée) (sans lever votre stylo) allant du coin inférieur gauche au coin supérieur droit (rouge) ou du coin supérieur gauche au coin inférieur droit (bleu) sans retour :vous dessinez de gauche à droite.
Le théorème du point fixe de Brouwer dit maintenant que ces fonctions ont un point fixe, c'est-à-dire que peu importe comment vous tracez cette ligne, il y aura certainement au moins 1 point dessus pour lequel la distance au côté gauche du carré est égale à la distance au côté inférieur. Les points du carré qui satisfont à cette exigence sont marqués en vert. En d'autres termes, le théorème dit que les fonctions bleue et rouge doivent couper la ligne verte quelque part, ce qui peut être clairement vérifié sur le dessin.

La déclaration ne dit rien sur l'emplacement de ce point fixe dans l'intervalle, ni sur le nombre de ces points fixes. La fonction bleue en a en effet exactement une, mais si vous regardez bien, vous pouvez voir que la fonction rouge en a même trois !
Pourquoi le nom point fixe ? Eh bien, nous pouvons le montrer en interprétant différemment les informations de la figure. Une hauteur est associée à chaque point sur l'axe horizontal (qui peut être lu sur l'axe vertical). Et si nous dessinons maintenant (par exemple dans le cas de la fonction bleue) ces deux axes différemment, vous pouvez voir dans la figure suivante via les flèches comment cette association se produit exactement. (A gauche l'axe horizontal, à droite la verticale.)
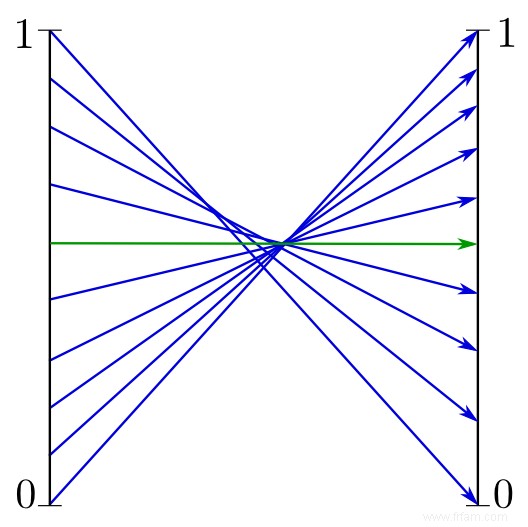
Et vous voyez qu'il y a un point à gauche qui se retrouve à la même hauteur à droite :la flèche verte. La hauteur reste la même :un point fixe ou point fixe ! Si la fonction est continue et que le graphique est ininterrompu, alors il existe toujours un tel point fixe. C'est ce que dit le théorème de Brouwer.
Pas encore assez concret ? Nous réessayerons. C'est les vacances, et on a envie de gravir une montagne. Vous partez en bas de la montagne (avec votre tente) à 10h, et vous remontez le chemin. A 18h vous avez atteint le sommet, vous profitez de la vue, mangez et buvez quelque chose, puis passez la nuit dans votre tente. Le lendemain matin, vous êtes prêt à descendre la montagne. Vous partez rapidement à 10h et descendez à pied. A 18h vous êtes de nouveau au pied de la montagne, à l'endroit où vous êtes parti la veille. Saviez-vous que vous pouvez maintenant être sûr qu'il y a un moment quelque part entre 10h et 18h où vous étiez à la même altitude lors de la montée (le premier jour) et de la descente (le deuxième jour) ? En effet, et vous pouvez facilement le voir aussi en utilisant un exemple. Prenez la figure avec la fonction bleue et la fonction rouge. Prenez l'axe horizontal comme axe du temps (avec l'unité 10h) et l'axe vertical comme axe des hauteurs (avec l'unité km), et supposons que la montagne mesure 1 km de haut. Vous pouvez alors voir la courbe rouge comme une représentation de l'ascension de la montagne (où il faut reculer un peu à cause de quelque chose de perdu en cours de route). La courbe bleue est pour le lendemain, la descente. Et nous nous sommes déplacés les deux jours l'un sur l'autre. Évidemment, les deux lignes doivent se croiser, quelle que soit la façon dont vous les dessinez. Ce point d'intersection indique le moment où vous étiez à la même hauteur lors de la montée et de la descente. Une conséquence du théorème de Brouwer.
Ce résultat s'applique également à plusieurs dimensions. En deux dimensions, par exemple, on peut penser à un disque rond (un disque plein, pas un CD) que l'on tourne d'un quart de tour. En effet, tous les points ont changé de position, sauf le point médian qui est donc notre point fixe conscient !
Bien que la formulation générale de ce théorème soit l'un des résultats les plus importants dans une partie très abstraite des mathématiques, ces néanmoins quelques belles applications dans la réalité. Pensiez-vous qu'il était possible de mélanger parfaitement une tasse de café avec un soupçon de lait en remuant avec une cuillère ? Erreur! Après avoir remué, lorsque le café s'est arrêté, il y aura toujours au moins une particule dans le liquide qui se retrouvera au même endroit qu'avant que vous ne commenciez à remuer. Une conséquence du théorème du point fixe de Brouwer (en supposant que l'agitation est un mouvement continu, que la tasse a une forme normale (convexe) et non exotique, et que le café n'est pas si chaud que le liquide ait pu s'évaporer entre-temps ) !
Une autre application est la suivante :prenez une carte du pays dans lequel vous vous trouvez. Posez simplement cette carte à plat sur la table. Il y aura alors, toujours grâce au théorème du point fixe de Brouwer, un Vous êtes ici ! point existe sur cette carte qui correspond exactement à l'endroit où vous vous trouvez dans la vraie vie. La logique elle-même, bien sûr. Nous le faisons à plus petite échelle. Obtenez un plan du village/ville où vous habitez, posez ce plan sur la table de la cuisine et cherchez sur ce plan la rue où vous habitez, plus précisément l'endroit où se trouve votre maison, plus précisément l'endroit où la cuisine est située (supposons que vous puissiez bien zoomer arbitrairement sur ce plan), plus précisément à l'endroit où se trouve la table dans votre cuisine. Dessinez un point là-bas. En dessous de ce point se trouve (a) votre table sur le plan (b) votre table dans votre maison. Donc un point fixe ! (Pour les puritains en mathématiques - vous devrez zoomer un peu plus pour bien faire les choses). Revenons à cette première étape du Tour de France :il y a donc (au moins) un point dans (pas forcément sur) le parcours de cette étape, à supposer qu'il s'agisse d'une réduction des contours de la Belgique, ce qui en soi s'affiche .

Un dernier fait remarquable est que le théorème du point fixe de Brouwer a également des liens avec des domaines mathématiques complètement différents, par exemple la théorie des jeux. En fait, cette position équivaut au jeu de plateau Hex ne peut pas se terminer par un match nul.

Le jeu Hex a été inventé dans les années 1940, indépendamment par le célèbre théoricien des jeux John Nash (le même que précédemment) et par Piet Hein (Piet Hein, son nom est petit, bien qu'il ne s'agisse pas de l'amiral néerlandais du flotte au trésor, mais à propos de son homonyme et descendant, le mathématicien danois).
Pour jouer au jeu, en plus d'un adversaire, vous avez également besoin d'un plateau composé de 11 par 11 tuiles hexagonales comme indiqué dans l'image ci-dessus. Les deux joueurs placent à tour de rôle une pierre de leur couleur (dans ce cas rouge ou bleue) sur le plateau, en essayant de relier d'abord les côtés de leur couleur au moyen d'une chaîne continue de pierres de la même couleur. Dans le jeu ci-dessous, le joueur bleu est le gagnant.
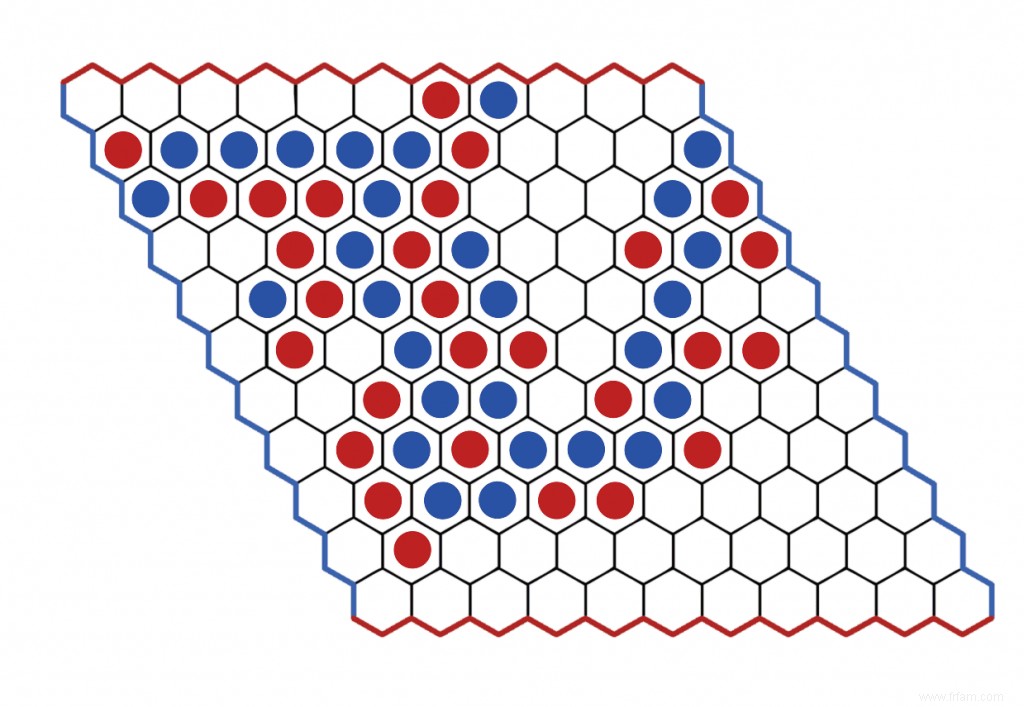
Le jeu Hex reste à ce jour l'objet de recherches mathématiques dans divers domaines. Ainsi, à ce jour, des stratégies gagnantes ont été développées pour tous les coups d'ouverture sur un tableau à 7\fois7$, un tableau à 8\fois8$ et un tableau à 9\fois9$. Bien que le jeu soit très facile à expliquer, la complexité est énorme. Il y a environ 2,4 $\times 10^{56}$ positions légales possibles, ce qui est bien plus que les 4,6\times 10^{46}$ possibilités aux échecs. Il y a donc beaucoup de stratégie pour terminer une partie en gagnant, et il faut être capable d'analyser des schémas très complexes afin de créer des connexions potentielles.
L'équivalence entre la décidabilité du jeu Hex et le théorème du point fixe de Brouwer n'est pas facile à démontrer (voir David Gale (1979). "The Game of Hex and Brouwer Fixed-Point Theorem." The American Mathematical Monthly. Association mathématique d'Amérique. 86 (10) p. 818-827). On peut montrer de manière relativement simple qu'une partie de Hex a bien toujours un vainqueur à la fin. Mais peut-être voulez-vous d'abord l'essayer vous-même ?
Sinon, un spoiler suit. Nous commençons avec un plateau de jeu complètement rempli dans lequel chaque tuile contient une pierre rouge ou bleue. Nous tracerons ensuite un chemin (en vert) entre les tuiles de différentes couleurs, en commençant par le coin supérieur gauche.
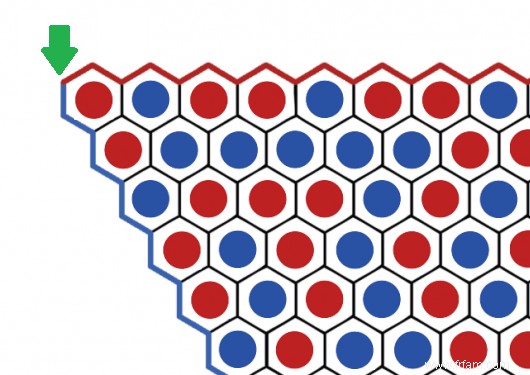
Considérez les bords du tableau comme des murs de pierres de la couleur respective. Dans notre exemple, le chemin descend pour les quatre premières marches, entre les pierres rouges et le mur bleu :
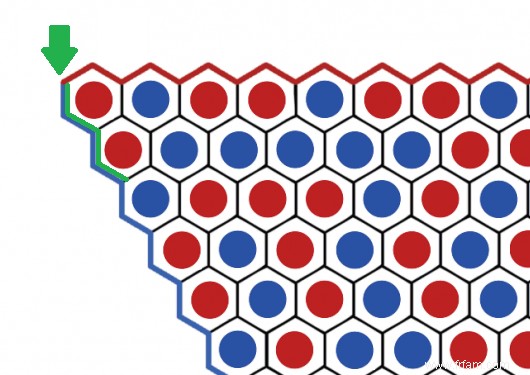
Après on change de direction, car on a toujours envie de côtoyer une pierre rouge et une pierre bleue en même temps. Le reste du chemin vert sur cette pièce du plateau de jeu est dessiné ci-dessous.

Nous pouvons maintenant noter quelques éléments :

Supposons, par exemple, que dans l'exemple présenté ici nous arrivions au fond entre la pierre rouge et la pierre bleue. Puisque les autres pierres autour de la pierre rouge du milieu sont toutes bleues, nous pouvons faire presque tout le tour avec notre chemin vert. Cependant, la dernière partie de la boucle ne peut pas être complétée, car nous arrivons à la pierre rouge inférieure et ne sommes pas autorisés à passer entre les deux pierres rouges avec la ligne verte.

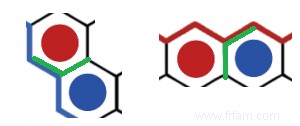
Ainsi, la seule option qui reste est que le chemin se termine dans l'un des autres coins du plateau de jeu.
Notez que les pierres à côté du chemin sont toujours rouges d'un côté et de l'autre côté. côté toujours bleu. Dans l'exemple ci-dessus, le côté gauche est rouge et le côté droit bleu, si l'on se place du point de vue du cycliste solitaire penché sur son guidon contre le vent, se faisant une voie verte, en partant de la flèche verte. Pour cette raison, le chemin vert ne peut jamais se terminer dans le coin inférieur droit, car nous devrions y arriver avec le rouge à droite et le bleu à gauche.

Cela laisse deux points finaux possibles, étant les deux coins restants du plateau de jeu. Supposons maintenant que le chemin se termine dans le coin inférieur gauche. C'est-à-dire que le mur bleu à gauche est complètement séparé du reste du plateau de jeu par une chaîne continue de tuiles rouges de l'autre côté du chemin vert. En d'autres termes, le joueur rouge a gagné. Voir ci-dessous un exemple fictif sur un tableau à 5 $ \ fois 5 $.

Dans le cas où le chemin se termine en haut à droite, bien sûr les rouleaux ont tourné et le bleu a gagné. Dans tous les cas, le plateau de jeu entièrement rempli contient quand même un gagnant.