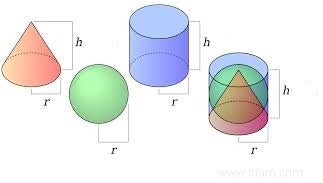
L'étudiant moyen se souviendra surtout d'Archimède de ses cours à l'école comme de l'homme nu qui a sauté de son bain alors qu'il était Eureka. s'écria, et pas tant qu'un mathématicien. Deux siècles après sa mort, Cicéron trouva la tombe d'Archimède et décrivit une pierre tombale avec un dessin en relief d'une sphère dans un cylindre. Cela peut être vrai car de toutes ses découvertes, Archimède était le plus fier de sa formule pour calculer le volume d'une sphère. En fait, il était particulièrement fier de la méthode avec laquelle il a pu comparer les volumes de la sphère, du cône et du cylindre.
La Scorpion est une arbalète surdimensionnée qui peut être armée par un tireur grâce à un multiplicateur de puissance mécanique. Avec cette plate-forme, la dernière saison de Game of Thrones un dragon de Daenerys Targaryen, abattu depuis le ciel pendant le siège de King's Landing † Ce fait fantastique a eu lieu en l'an 304.
Peu de fans de ce fantasy sachez que le Scorpion fut utilisé par les Romains dès le début de notre ère, et probablement même par l'armée du roi Ozias de Juda au VIIIe siècle av.
Mais cette ingéniosité mécanique m'a surtout rappelé le célèbre mathématicien grec Archimède , né à Syracuse (287 av. J.-C.), où en 212 av. a été assassiné pendant la seconde guerre punique par un soldat romain. Selon l'historien Tite-Live, cela s'est produit après l'irritation d'Archimède parce que le Romain maladroit a marché sur une figure géométrique dessinée dans le sable sur le sol. Selon la même Tite-Live, « Ne dérangez pas mes cercles » furent les derniers mots d'Archimède. Parfois, les mathématiques sont irresponsablement intéressantes.

Cependant, le commandant romain Marcus avait explicitement ordonné à Marcellus de capturer Archimède vivant. Après tout, Archimède était une légende vivante à son époque pour ses inventions d'outils (comme la pompe à vis ) et des dispositifs militaires (variantes de la catapulte et du scorpion, de la griffe, des miroirs solaires,…). Ces armes ont permis à Syracuse de résister au siège romain pendant deux ans. Dans l'Antiquité, il était également célèbre pour ses découvertes de principes physiques en statique (règle de levier) et en hydrostatique (poussée vers le haut), tandis que ses connaissances mathématiques n'ont pénétré la science que progressivement des siècles plus tard. Ses contemporains admiraient Archimède pour avoir submergé la couronne du roi de Syracuse dans l'eau, prouvant que l'orfèvre n'avait pas utilisé d'or pur.
Mais presque personne ne savait qu'il (le premier) pouvait calculer avec précision le nombre $\pi$ approche , et qu'il pouvait calculer exactement l'aire des régions paraboliques, à propos en utilisant des techniques limites et intégrales qui n'ont été inventées que 2000 ans plus tard. Même aujourd'hui, l'élève moyen de ses classes se souviendra surtout d'Archimède comme de l'homme nu qui a sauté de son bain alors qu'il était Eureka. s'écria, et pas tant qu'un mathématicien. Deux siècles après sa mort, Cicéron visita la ville de Syracuse et partit à la recherche du tombeau d'Archimède. À l'exception du soldat qui s'est essuyé les pieds sur le cercle en question, presque tous les Romains étaient fans d'Archimède. Selon ses propres mots, Cicéron a trouvé cette tombe efficace. L'orateur romain décrit une pierre tombale avec un dessin en relief d'une sphère dans un cylindre. Cela peut être vrai car de toutes ses découvertes, Archimède était le plus fier de sa formule pour calculer le volume d'une sphère. En fait, il était particulièrement fier de la méthode avec laquelle il a pu comparer les volumes de la sphère, du cône et du cylindre. Et cette fierté était plus que justifiée !
Bien sûr, mon association est entre le Scorpion de Game of Thrones et les inventions d'Archimède fortement influencées par un récent voyage de vacances à Syracuse, où j'ai eu moins de chance que Cicéron, car je n'ai pas trouvé la vraie tombe d'Archimède, seulement une réplique pour plaire aux touristes. Mais je recommande à tous de visiter TechnoParco, une sorte de parc d'attractions d'Archimède.

Quiconque devait se laver à terre dans ce petit musée en plein air confortable ne devrait certainement pas manquer de laisser le propriétaire déballer ses connaissances sur le puzzle d'Archimède Stomachion.

La méthode délibérée d'Archimède est une combinaison de couper un objet en fines tranches (la méthode d'épuisement ), associé à son principe de levier. En fait, nous ne le savons que depuis le début du siècle dernier, lorsque le Danois Johan Ludvig Heiberg à Constantinople a étudié un parchemin qui avait été recyclé et qui contenait sous les couches supérieures une lettre originale d'Archimède à son ami Eratosthène de Cyrène .
Visualisons d'abord le principe du levier, dont Archimède est bien l'auteur. L'éléphant ci-dessous pèse 100 000 fois plus que la souris, mais la bascule est équilibrée car la souris est 100 000 fois plus éloignée du point d'appui F que l'éléphant. Le produit du poids et de la distance est égal des deux côtés du point d'appui.
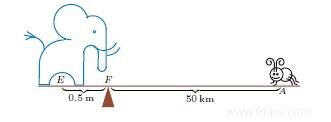
Il est important ici que la distance au point d'appui soit toujours mesurée à partir de la position du centre de gravité de l'objet (souris, éléphant ou autre). Dans son argumentation, Archimède utilisait généralement des objets homogènes qu'il supposait tous faits du même matériau (même densité), de sorte que le rapport des poids de deux objets est égal au rapport de leurs volumes. Ainsi, l'équation d'équilibre d'une balance peut être formulée sous la forme $V_1\times d_1 =V_2\times d_2$, pour des corps de volumes $V_1$ et $V_2$, et de distances respectives $d_1$ et $d_2$ du support.
Ensuite, nous sommes arrivés à la méthode d'épuisement , qui peut à juste titre être considéré comme le tout premier calcul intégral, bien que l'invention de l'intégrale dans les manuels d'Analyse soit généralement attribuée à Newton ou à Leibniz (selon que l'auteur parle la langue de Shakespeare ou de Goethe). Dans la lettre que Heiberg rapporta à la surface, Archimède attribua entièrement le mérite de cette méthode à Démocrite (460-370 av. J.-C.). Ce dernier était aussi assez ingénieux, à tel point qu'un Platon jaloux proposa un jour de brûler tous ses écrits. En fait, Archimède a été le premier à obtenir de nouveaux résultats avec la méthode d'épuisement.
Préparez-vous maintenant à une confrontation avec le génie stupéfiant avec lequel Archimède comparait les volumes de la sphère, du cylindre et du cône. Prenez un cylindre, un cône et une sphère comme dans la figure ci-dessous. Nous étudions la situation où le rayon et la hauteur du cylindre sont égaux au diamètre de la sphère, et où le cône s'emboîte correctement dans le cylindre. Si nous écrivons $r$ pour le rayon de la sphère, alors le rayon de la base circulaire du cône et du cylindre est égal à $2 r$. De plus, la hauteur $h$ du cône est égale à celle du cylindre et également égale au diamètre $2 r$ de la sphère.
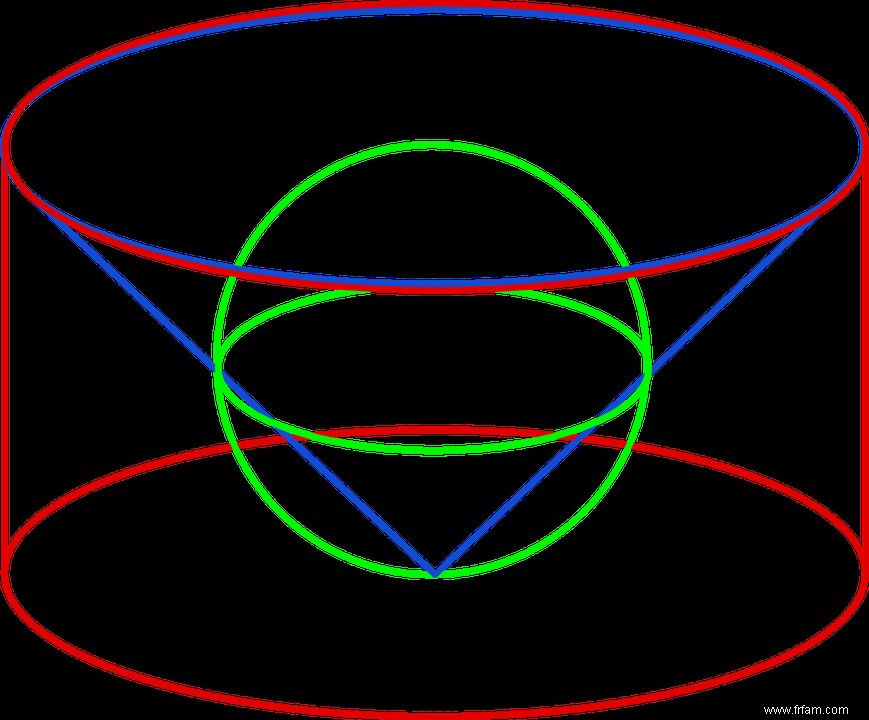
Dans cette expérience de pensée, le cylindre est placé sur le côté sur une bascule (horizontale) avec un point d'appui en $A$ (voir figure). Cette bascule peut être un axe sur lequel le cylindre a été glissé en brochette, ou simplement une étagère sur laquelle repose le cylindre, peu importe.
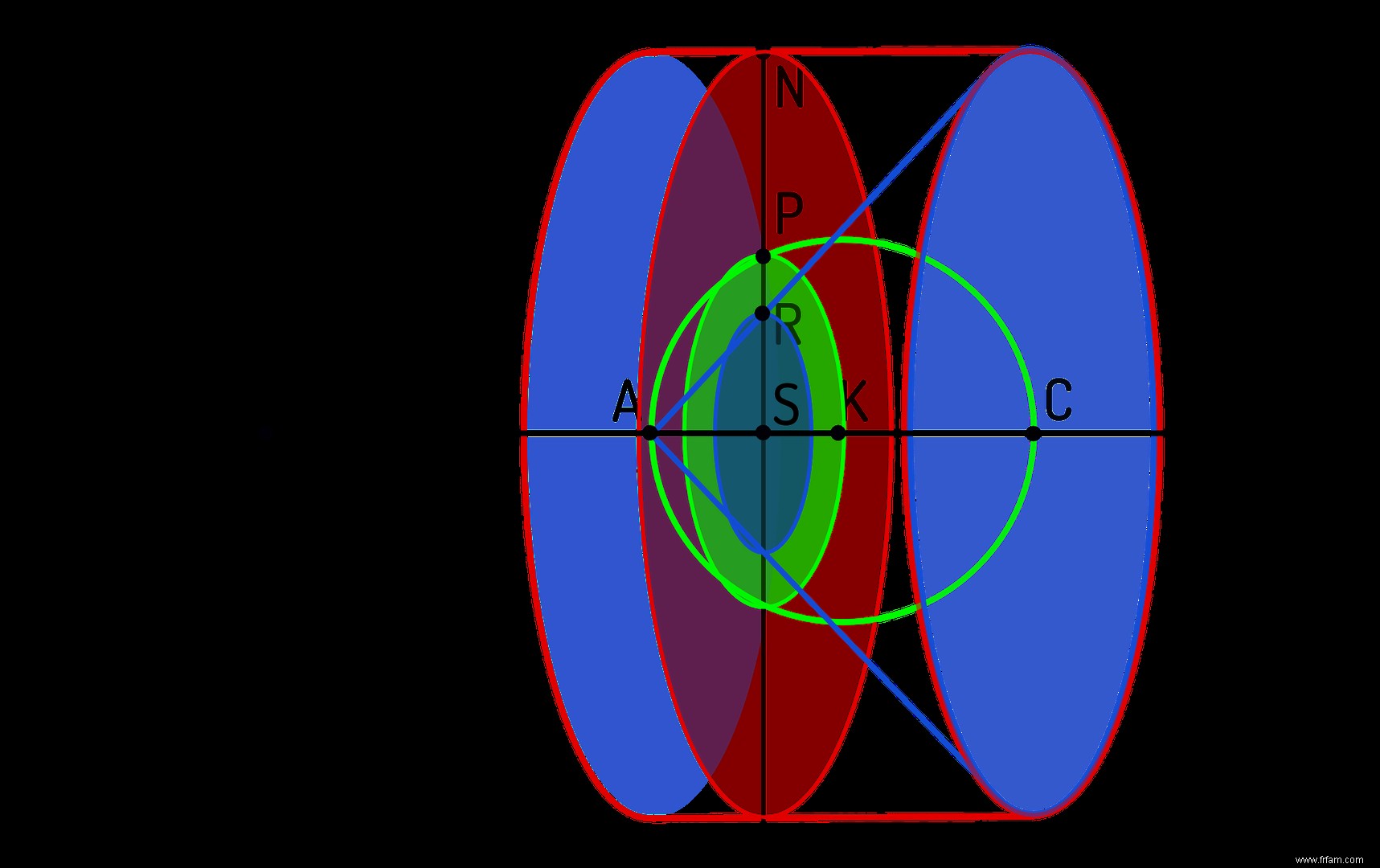
Il est important que les sections circulaires du cylindre soient perpendiculaires à la bascule, avec la base au point d'appui $A$. La face supérieure est en position $C$ de la bascule à une distance de $2 r$ de $A$, car la hauteur du cylindre est égale au diamètre de la sphère. Dans notre esprit on place le cône dans ce cylindre (ce qui fonctionne correctement, et d'une seule façon), et on imagine aussi la sphère dans le cylindre, telle que l'axe du cylindre ( $=$ axe du cône) coïncide avec un diamètre du sphère. Heureusement, il s'agit d'une expérience de pensée car il est pratiquement impossible de presser le cône et la sphère dans le cylindre en même temps.
Maintenant, la méthode d'épuisement entre en jeu, dans laquelle Archimède coupe ces trois objets en fines tranches, perpendiculaires à l'axe du cylindre, de gauche à droite (c'est-à-dire de $A$ à $C$). A tout moment, nous découpons simultanément 3 tranches de nos objets :un disque cylindrique, un disque sphérique et un disque conique. Il faut se représenter ces disques comme les pierres d'un jeu de palets (voir figure), et sont donc eux-mêmes cylindriques, bien que très plats, avec une faible hauteur ($=$ épaisseur du disque). En toute rigueur, seul le disque cylindrique a une arête perpendiculaire au plan de coupe, alors que l'arête d'un disque conique est oblique et celle d'un disque sphérique est courbée, mais si on taille nos disques assez fins ces écarts sont négligeables.

L'homme moderne a des notions de concept limite et d'infinitésimaux , mais à cette époque c'était tout un tour de force de travailler avec des tranches dont l'épaisseur est infiniment petite, mais pas nulle. Ils ont donc un volume, comme les disques de palets, à savoir l'aire de l'intersection circulaire multipliée par l'épaisseur (infinitésimale) $\delta$. Soit dit en passant, la formule de l'aire d'un cercle était connue d'Archimède (et prouvée !), étant $\pi$ fois le carré du rayon.
Supposons que notre slicer soit en position $S$, à une distance de $x$ du point d'appui $A$ (voir figure). Les 3 tranches que nous coupons simultanément ont bien entendu des rayons différents :
Or Archimède avait l'idée que le disque du cylindre dans n'importe quelle position de coupe $S$ est équilibré si nous plaçons les deux autres disques (tels que découpés à l'endroit $S$) au point $H$, ce point étant $H$ à un distance de $2r$ du point d'appui $A$.
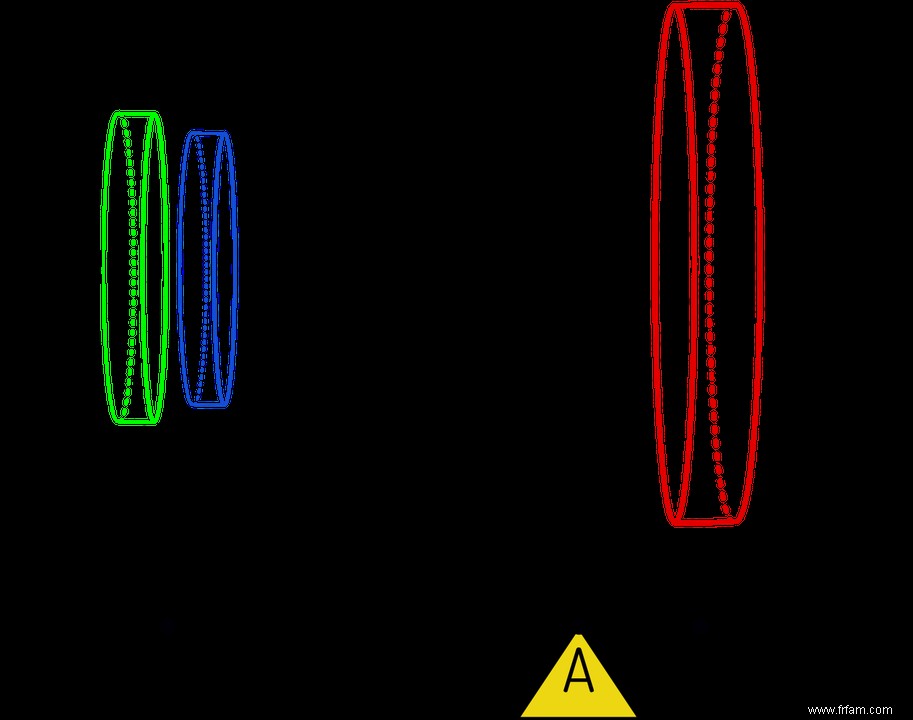
Le lieu $S$ varie de $A$ à $C$, tandis que le point $H$ est fixe, mais bien sûr le cône et le disque sphérique ne cessent de grossir. Le lecteur peut avoir du mal à placer deux pions en 1 point minuscule, mais nous voulons dire que le centre de gravité des deux pions doit être à $H$. L'équilibre découle du calcul du rapport des deux volumes (de droite à gauche) :
$$\frac{V_1}{V_2} =\frac{\mbox{vol(disque cylindrique)}}{\mbox{plein(disque conique)}+\mbox{plein(disque sphérique)}}$$
Parce que Si 3 tranches ont la même épaisseur (infinitésimale) $\delta$, le rapport $V_1/V_2$ peut être considéré comme le rapport des aires des sections circulaires. Comme $\pi$ est un facteur commun, on peut même se limiter aux carrés des rayons pour calculer ce rapport :
$$\frac{V_1}{V_2} =\frac{4 r^2 }{ x^2 + (2rx – x^2)}=\frac{4 r^2}{2rx}=\frac{2 r}{x},$$
qui est identique au rapport des distances support du centre de gravité (de gauche à droite) :
$$\frac{d_2}{d_1} =\frac{2r}{x},$$
de sorte qu'à chaque intersection $S$ on avoir un équilibre selon le principe du levier.
La conclusion de la méthode d'épuisement est qu'un équilibre global découle des équilibres locaux par tranche. En d'autres termes :
Le cylindre, complètement coupé (épuisé ) comme il est compris entre $A$ et $C$, il est équilibré par rapport au point d'appui $A$ par le cône et la sphère reconstruite à gauche au point $H$.
Peu importe comment le cône et la sphère sont correctement positionnés, tant que leur centre de gravité commun est au point $H$. D'autre part, par symétrie, le centre de gravité du cylindre est juste au centre du cylindre, ce qui correspond à la position $r$ sur la bascule. Cet équilibre global signifie donc que
$$\left({\mbox{vol(cône)} + \mbox{vol(sphère)}}\right)\cdot 2r =\mbox{vol(cylindre)}\ cdot r$$
ou
$$\mbox{vol(sphère)} =\frac{1}{2} \left({\mbox{plein(cylindre)} – 2\cdot\mbox {plein(cône)}}\right)$$
Or Archimède savait que le volume d'un cône n'est qu'un tiers du volume d'un cylindre ayant la même hauteur et la même base que le cône. Par exemple, ceci est énoncé comme Proposition 10 dans le Livre XII du Livre d'Euclide. De notre équilibre cône-sphère-cylindre, il s'ensuit que le volume d'une sphère est $1/6$ du volume du cylindre avec une hauteur et un rayon égaux au diamètre de la sphère. Le volume d'un tel cylindre (hauteur $=$ rayon $=2r$) est égal à $8 \pi r^3$, et donc celui de la sphère $\frac{4}{3}\pi r^3$.
Pour les étudiants d'aujourd'hui, dériver cette formule de contenu est un exercice standard de calcul intégral, mais la réussite d'Archimède restera toujours d'un ordre supérieur, car il a directement lié le contenu de la sphère, du cône et du cylindre. Le résultat d'Archimède est aussi une forme de mesure plus pure, car il n'utilise pas la théorie de la mesure ni les constructions intégrales !