Maintenant que le soleil brille plus souvent, vous pouvez voir de beaux paysages partout dans la nature. Comme celui-ci :

ou celui-ci, avec une tasse de café :

Une version améliorée est obtenue à l'aide d'un anneau de garniture (voir ci-dessus).
C'est la courbe dessinée par le soleil, qui est créée par la réflexion de la lumière dans l'anneau de garniture cylindrique. Il est connu sous le nom de Coffeecup Caustic. Cette courbe est appelée catacoustique et a été étudiée par les mathématiciens il y a longtemps. J'ai longtemps cru que Christiaan Huygens (1629-1695) était le premier, dans son Traité de la lumière (1678).
Le nom kaustiek a été donné par Ehrenfried Walter von Tschirnhaus (1651-1708) et est dérivé du mot grec signifiant « brûler ». En néerlandais on peut parler de courbe de feu, par analogie avec le foyer, par exemple, d'une parabole (où les rayons lumineux incidents parallèlement à l'axe sont réfléchis par ce point unique, du moins si la parabole est spéculaire).
Von Tschirnhaus est surtout connu pour l'invention de la porcelaine, mais il a également fabriqué de grands « miroirs à feu » avec l'intention de produire des températures très élevées. D'où son intérêt pour ce sujet. Le fait qu'Archimède avait également un œil pour les courbes de feu ressort de l'histoire du siège de Syracuse pendant la seconde guerre punique, dans laquelle il est dit qu'Archimède a mis le feu à la flotte romaine à l'aide de grands miroirs en bronze.
J'ai été très surpris lorsque je suis tombé sur le chiffre suivant il y a quelques jours :
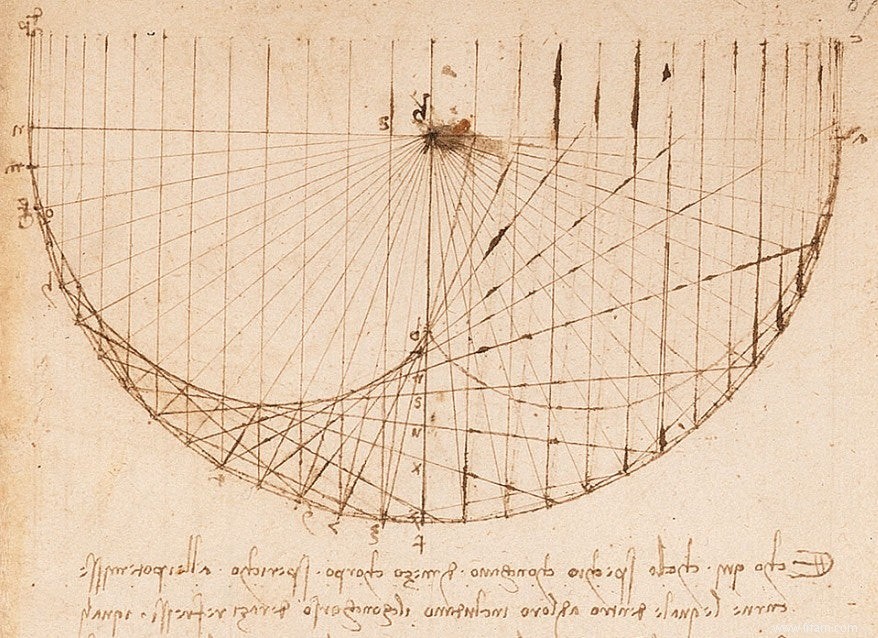
dans l'un des cahiers de Léonard de Vinci (1452-1519), à savoir le Codex Arundel, du début du XVIe siècle. Une version moderne de ce dessin ressemble à ceci :
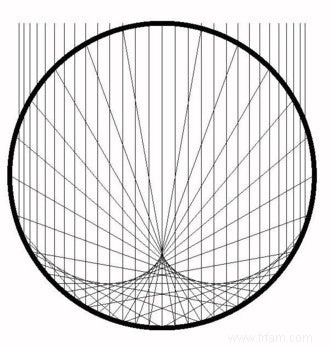
Mais de quelle courbe parle-t-on ici ? Dans le dessin, vous pouvez voir que la courbe que vous recherchez est tangente aux rayons réfléchis. En mathématiques on parle d'enveloppe des rayons réfléchis. Les méthodes pour trouver l'équation d'une enveloppe existent depuis longtemps. Dans ce cas, il s'agit d'une demi-courbe rénale, ou néphroïde, courbe qui appartient aux épicycloïdes. Ce sont des courbes qui apparaissent lorsqu'on fait rouler un cercle autour d'un cercle fixe sans glissement, et qu'on suit le mouvement d'un point sur le bord du cercle roulant :
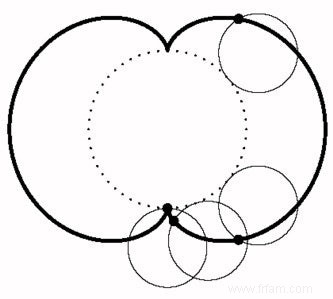
Au fil des siècles, les bilans ont été étudiés par des mathématiciens non des moindres, par certains Bernoulli par exemple, mais aussi par Adolphe Quételet (1796-1874), mathématicien natif et connu des statistiques et « inventeur » de l'indice de masse corporelle.
Si vous travaillez dessus pendant un certain temps, vous vous retrouverez bientôt dans un monde plein de courbes aux noms exotiques tels que les développées, les développantes, les courbes des points de pied, les orthotomiques. Avec de belles images aussi. Par exemple, la caustique d'une cycloïde est à nouveau une cycloïde de la moitié de la taille de l'original :
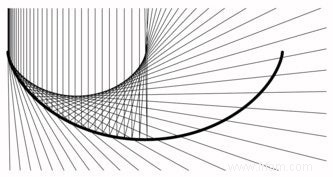
Et la caustique de la fonction exponentielle bien connue est une autre courbe célèbre, à savoir la chaînette :
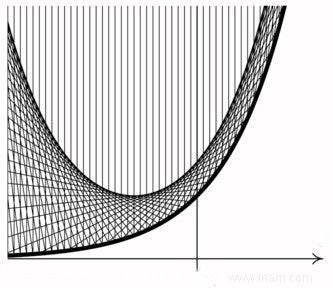
Je peux recommander aux lecteurs intéressés le livre de Johann Bernoulli (1667-1748) (ici dans une traduction allemande), les chapitres sur les caustiques commencent à la page 110, ou le premier vrai livre de Calcul, écrit par Guillaume de l'Hospital (1661- 1704) (à partir de la page 148 il s'agit de caustiques). Les évaluations sont encore à l'étude aujourd'hui, par exemple dans le secteur de l'infographie (dans lequel le collègue blogueur Philip Dutré est actif).
Voici une image entièrement générée par l'ordinateur :

Et cela rentre complètement dans le cadre :

Ressources/en savoir plus