Il est surtout connu pour la suite de nombres qui commence ainsi :1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670 et ceux de multitudes de problèmes surgissent de toutes sortes. Pour donner un exemple :de combien de manières pouvez-vous placer $n$ (paires) de parenthèses (c'est-à-dire (...)) dans un produit avec $n+1$ facteurs ? Ici on regarde le placement des parenthèses comme on le fait traditionnellement en mathématiques :on les met de manière économique, un seul facteur n'est jamais entre parenthèses, mais tous les facteurs ensemble le sont.
Un exemple, pour $n=2 $ , donc 2 paires de parenthèses, avec 3 facteurs :
$$((ab)c),(a(bc))$$
Donc seulement deux façons :c'est le troisième nombre de la suite.
Pour $n=3$, avec 4 facteurs, les possibilités sont :
$$(((ab)c)d),((a(bc))d),(a((bc)d)),(a(b(cd))),((ab)(cd)) $$
Donc cinq. Et ça continue comme ça.
Supposons que vous êtes assis à une table ronde (pas trop grande) avec un nombre pair de personnes (2n$). De combien de façons la moitié du groupe peut-elle simultanément serrer la main à quelqu'un d'autre à cette table, éventuellement de l'autre côté de la table, sans provoquer de croisement ?

En effet, vous retrouverez les mêmes numéros.
Combien de façons pouvez-vous empiler des pièces (comme des oranges, mais en 2 dimensions !) si vous commencez avec une rangée inférieure de $n$ pièces ? Vous pouvez le voir ici pour $n=3$.

Il y en a 5, et vous pouvez vérifier vous-même que vous obtenez la même rangée de chiffres. De plus, le nombre de façons différentes de diviser un angle $n$ régulier en triangles non superposés est décrit avec cette rangée de nombres :pour un triangle 1 façon, pour un carré 2 , pour un pentagone il y en a 5 , etc.
(Vous pouvez en savoir plus sur le lien étrange entre de telles triangularisations de polygones et des motifs de frise ici. Cet article est sur un site Web intéressant, bien que pour les personnes ayant une formation en mathématiques. Le site Web est également lié au projet imaginaire, et ainsi de suite avec une exposition récemment arrivée en Flandre.)

Cette suite de nombres est appelée la suite des nombres catalans, du nom du mathématicien français Eugène Charles Catalan (1814-1894) né à Bruges, mort à Liège. Et si Napoléon avait été vaincu un an plus tôt, le catalan n'aurait pas été français ! Bruges a fait partie de la France de 1799 à 1815...
Dommage, car le catalan n'en était pas le moindre en tant que mathématicien. Dans l'encyclopédie concise des mathématiques du CRC (3242 pages) vous trouverez des informations sur les intégrales catalanes, les nombres catalans (!), les polyèdres catalans dont celui-ci fait partie :

Conjecture aliquote de Catalan, conjecture de Catalan (les nombres 8 et 9 sont les seules puissances (23,32) qui ne diffèrent que d'une unité l'une de l'autre - en attendant un théorème car prouvé en 2002 par Preda V. Mihăilescu), la constante de Catalan :
$$G=\sum_{n=0}^\infty \frac{(−1)^n}{(2n+1)^2}$$
l'identité du catalan pour les nombres de Fibonacci, l'aire minimale du catalan :

le triangle de catalan, et enfin la trisectrice de catalan. Pas mal comme récolte.
La famille de Catalan déménagea bientôt à Paris, où Eugène fréquenta l'école à l'École Royale Gratuite de Dessin et de Mathématiques et Faveur des Arts Mécaniques. A partir de 1829 (!), il y donne également des cours de géométrie. En 1833, il entre à l'École polytechnique, époque à laquelle la politique commence à lui jouer des tours. C'était un républicain convaincu à une époque où il valait mieux ne pas l'être. Il a été expulsé pendant un mois, mais a quand même obtenu son diplôme en 1836, puis a continué à enseigner. Dès lors, la carrière mathématique de Catalan a commencé. De nombreux articles mathématiques, de nombreux prix, et bien des pérégrinations plus tard, Catalan devient professeur à l'Université de Liège, où il déclare ceci en 1881 lors de la fête de sa retraite :
Deux passions, Messieurs, ont surtout rempli ma vie :la Politique militante et la Mathématique, comme on disait autrefois. Un discours sur la politique serait de mauvais goût, serait déplacé dans cette enceinte. Puis, nous ne serions peut-être pas d'accord, vous et moi. Il n'en sera pas de meme, j'en suis convaincu, si je soumets à mes chers élèves, anciens et nouveaux, non une Dissertation sur les délices des Mathématiques (cela nous mènerait trop loin), mais quelques réflexions, bien simples, parents au travail intellectuel.
(Si vous lisez ce qui est en gras, il nous semble que le catalan était un homme selon nos cœurs.)
Si vous voulez en savoir plus sur les chiffres du catalan, prenez le temps de regarder cette vidéo.
Nous aimerions en profiter pour revenir sur l'un de nos sujets favoris :les nombres parfaits et leurs parents. L'autre conjecture de Catalan, la conjecture aliquote, n'est toujours pas résolue.
Les rangées de nombres suivantes sont ce qu'on appelle des rangées aliquotes. Le premier numéro de la ligne détermine complètement le cours ultérieur de cette ligne. (Voir ci-dessous pour une explication de la manière exacte.)
1 , 0.
2 , 1, 0.
3 , 1, 0. (C'est ainsi que ça se passe à chaque fois que vous commencez avec un nombre premier)
4 , 3, 1, 0.
5 , 1, 0.
6 , 6, 6, ... (c'est comme ça à chaque fois que vous commencez avec un nombre parfait)
8 , 7, 1, 0.
9 , 4, 3, 1, 0.
12 , 16, 15, 9, 4, 3, 1, 0.
14 , 10, 8, 7, 1, 0.
25 , 6, 6, 6, ... (c'est comme ça quand on tombe sur un nombre parfait dans la rangée)
28 , 28, 28, ... (encore un nombre parfait)
30 , 42, 54, 66, 78, 90, 144, 259, 45, 33, 15, 9, 4, 3, 1, 0.
220 , 284, 220, 284, 220, ... (c'est comme ça si vous commencez par un nombre qui appartient à une paire de nombres amis)
1264460 , 1547860, 1727636, 1305184, 1264460, .... (c'est toujours comme ça quand on commence par un nombre qui appartient à un groupe de nombres cosy)
La ligne est créée comme suit. On commence par un nombre positif, et on détermine les vrais diviseurs de ce nombre, qui sont tous des diviseurs sauf le nombre lui-même. La somme de ces diviseurs réels est le nombre suivant dans la séquence. Nous faisons exactement la même chose pour cela.
Un exemple. Nous commençons par 12 , avec diviseurs réels 1,2,3,4,6 avec somme 1+2+3+4+6 =16 † C'est le deuxième chiffre de la rangée. Les vrais diviseurs de 16 ont la somme de 1+2+4+8 =15 , le troisième nombre. 15 devient 1+3+5 =9 , 9 devient 1+3 =4 , 4 devient 1+2 =3 , 3 devient 1 , et 1 donne 0 car 1 n'a que lui-même comme diviseur. Puis ça s'arrête.
Quelques réflexions à ce sujet :

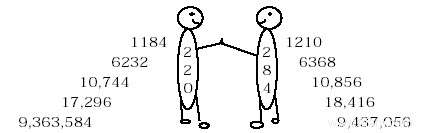
La suite devient alors périodique, de période 2.
La conjecture aliquote de Catalan indique que ce sont les seules options. C'est-à-dire qu'il ne peut arriver qu'une suite continue indéfiniment sans devenir constante ou périodique :
Comme vous pouvez le lire, le catalan a oublié certains cas. Cela a été compensé par Leonard Eugene Dickson.
Cette conjecture est-elle vraie ? Paul Erdős, par exemple, ne le pensait certainement pas. Depuis l'avènement des ordinateurs puissants, beaucoup a bien sûr été calculé pour ce problème. Et pourtant il reste encore cinq nombres inférieurs à 1000 dont la séquence correspondante se termine. On les appelle les cinq de Lehmer :276, 552, 564, 660 et 966. Catalan n'a probablement pas réalisé ce qu'il a provoqué avec ces quelques lignes dans le Bulletin de la Société Mathématique de France.
On termine avec deux belles formules du catalan, pour les nombres pi et e :
$$\frac{\pi}{2\sqrt{2}}=\frac{4\cdot4}{3\cdot5}\cdot\frac{8\cdot8}{7\cdot9}\cdot\frac{12\ cdot12}{11\cdot13}\cdot\frac{16\cdot16}{15\cdot17}\cdot\ldots$$
$$e=\frac{2}{1}\left(\frac{4}{3}\right)^{1/2}\left(\frac{6\cdot8}{5\cdot7}\right) ^{1/4}\left(\frac{10\cdot12\cdot14\cdot16}{9\cdot11\cdot13\cdot15}\right)^{1/8}\ldots$$
Enfin ça. Honneur à tout crédit :le 18 juin 2065, nous bloguerons sur la thèse de Napoléon.
