Le 6 novembre de cette année, il a été rendu public que le Hongrois Peter Szabolcs avait trouvé un nouveau nombre premier le 31 octobre :10223×231172165+1. Avec ses 9383761 chiffres, c'est le septième plus grand nombre premier jamais découvert par l'homme.

Le 6 novembre de cette année, il a été rendu public que le Hongrois Peter Szabolcs avait trouvé un nouveau nombre premier le 31 octobre :10223×+1. Avec ses 9383761 chiffres, c'est le septième plus grand nombre premier jamais découvert par l'homme. Mais c'est le plus grand Proth prime connu , c'est-à-dire un nombre premier de la forme k× avec koneven. Et c'est le seul parmi les 10 plus grands nombres premiers connus qui n'a pas de Mersenne premier est un nombre premier de la forme 2n−1. (consultez La plus grande base de données de nombres premiers connus par Chris Caldwell).
De plus, cette nouvelle trouvaille de Szabolcs est le plus grand nombre de Colbert jusqu'à maintenant. Il s'agit d'un méga nombre premier (un nombre premier avec plus d'un million de chiffres) sous la forme Proth k×2+1 où k appartient aux 17 nombres de la liste de Dix-sept ou Bust † Puisque k=10223 figure bien sur cette liste, ce nouvel ajout bien membré à la famille des nombres premiers est donc appelé un nombre de Colbert, du moins par certains mathématiciens bizarres flirtant avec la folie (par commodité, nous ferons semblant de vous poser la question " Y en a-t-il d'autres? n'en ont pas entendu parler). Le nom fait référence à Stephen Colbert , l'hôte de la populaire émission humoristique américaine The Colbert Report † Cet homme n'a rien à voir avec l'affaire, mais c'est un gag courant pour les gens qui inventent des noms pour nommer toutes sortes de choses après lui, de préférence s'il n'y a aucun lien avec Colbert. Un pont en Hongrie, un avant-goût de Ben&Jerry, une araignée en Californie,…, et maintenant aussi une famille spéciale de méga primes.
Mais la découverte récente de Szabolcs est particulièrement intéressante car nous savons maintenant que 10223 aucun Numéro Sierpinski est, et que donc seuls 21181, 22699, 24737, 55459 et 67607 sont encore en lice pour le numéro Selfridge 78557 pour être dépouillé de son statut de plus petit numéro Sierpinski. Si le lecteur se sent écrasé par cette quantité d'informations dénuées de sens et de chiffres mystiques, nous pouvons immédiatement le rassurer. C'était l'intention. Mais lisez la suite, les choses seront expliquées. Si à la fin tout n'est pas devenu clair, au moins on aura compris que tout le monde n'a pas la même idée des passe-temps utiles.
PrimeGrid, le réseau mondial de chasseurs de nombres premiers et de puissance de calcul groupée, est peut-être même geek , encore plus sombre et plus lâche du monde que la communauté des joueurs qui ne dort jamais. Une grande partie du temps de calcul de PrimeGrid est consacrée au projet GIMPS, qui se limite à la recherche de nombres premiers de Mersenne (de la forme 2-1), une stratégie réussie comme en témoignent les records battus pour les plus grands nombres premiers des 25 dernières années, qui tous avaient une forme de Mersenne. Le lecteur pourra se rafraîchir la mémoire en relisant notre article de blog de début 2016 à l'occasion du dernier record (toujours au nom de Cooper, un nombre premier de plus de 22 millions de chiffres).
Mais maintenant, nous aimerions attirer votre attention sur une autre "sous-culture" au sein de PrimeGrid, les chevaliers de la nuit du projet Seventeen or Bust , officiellement fermé en avril 2016, mais certains échos tenaces ont continué à résonner dans les caves sombres de PrimeGrid depuis. Dans ce sous-projet, les nombres premiers de la forme k⋅2+1 sont chassés, appelés Proth premiers † Vous commencez toujours par un nombre impair k, par exemple k=9, multipliez-le par 2 ou une puissance de 2, par exemple 9×2=18, et ajoutez un, par exemple 18+1=19. Dans cet exemple, nous avons de la chance, car nous trouvons un nombre premier (Proth) 19. Plus vous voulez de chiffres pour votre nombre premier Proth, plus vous devrez chercher longtemps. En fait, avec un peu de chance, vous choisissez un nombre malchanceux k comme valeur initiale pour laquelle k⋅2+1 ne devient jamais premier, pas pour deux puissances de 2n.
En 1960, le mathématicien polonais Waclaw Sierpinski qu'il existe même un nombre infini de tels nombres (impairs) k qui ne conduisent jamais à un nombre premier de Proth k⋅2+1. Ces choix "malheureux" pour la valeur initiale k devinrent désormais des nombres de Sierpinski. Nommé. Savoir qu'il y en a une infinité est une chose, mais effectivement trouver un numéro Sierpinski (avec preuve de garantie) en est une autre. En 1962, l'américain Selfridge a prouvé que 78557 est un nombre Sierpinski. Il l'avait étudié pendant si longtemps qu'il supposait qu'il s'agissait du plus petit nombre de Sierpinski. À l'époque où les capacités informatiques étaient limitées, c'était une supposition farfelue, mais maintenant la plupart des mathématiciens pensent qu'il avait raison. En janvier 2002, presque tous les nombres k inférieurs à 78557 s'étaient avérés donner lieu à un nombre premier de la forme k⋅2n+1 (et n'avaient donc pas la propriété de Sierpinski), mais il restait dix-sept candidats difficiles pour les propriétés de Sierpinski. supérieur à 78557, ce qui pourrait donc contredire la conjecture de Selfridge. Louis Helm, Ann Arbor et David Norris, deux étudiants en informatique et un programmeur du Michigan (peut-être tous les trois avec la « queue de cheval » obligatoire) ont voulu régler cette affaire une fois pour toutes. En mars 2002, sous leur impulsion, Seventeen or Bust voit le jour, un réseau informatique qui distribue les calculs aux processeurs de plus d'un millier de volontaires, avec l'intention de supprimer un à un la liste des 17 nombres de Sieprinski possibles. Une activité comme une autre, disons-le, quelque chose de différent que d'éviter les boules de Noël lancées par Lemma Koopa avec Super Mario.
En quatorze ans de ce projet, Seventeen ou Bust avait réussi à exposer 11 des 17 candidats restants pour un nombre de Sierpinsky inférieur à 78557. Les six restants étaient :10223, 21181, 22699, 24737, 55459 et 67607.
Ceux qui sont à l'affût comprennent qu'un candidat k est éliminé dès qu'un nombre premier de Proth associé k⋅2n+1 est découvert . C'était et c'est un travail difficile et chronophage car ce n'est pas pour rien que cette liste contient le dernier des candidats Sieprinsky plus petit que 78557. Le nombre premier Proth pertinent est donc d'une longueur considérable, mais après le test premier positif rédempteur, il reçoit le titre honorifique de nombre de Colbert.
En octobre 2016, grâce au travail de la communauté Seventeen or Bust, Szabolcs a obtenu un concurrent pour déposer 10223, l'éventuel nombre Colbert 10223×231172165+1. Il a utilisé une implémentation pratique du test principal LLR et près de neuf jours de temps de calcul sur son processeur Intel Core i7-4770 à 3,40 GHz avec 12 Go de RAM pour finalement confirmer ce cas.
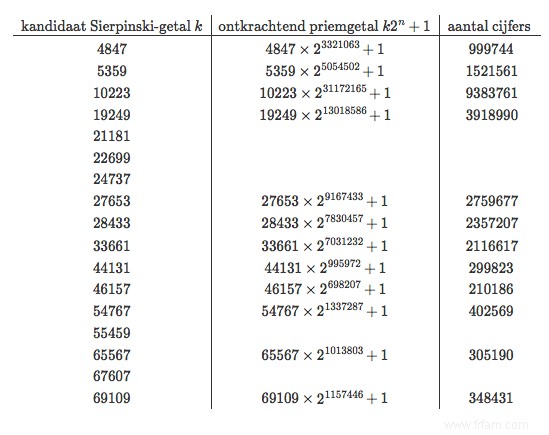
Dans un souci d'exhaustivité, nous donnons ci-dessous la liste des 17 valeurs de k qui se trouvaient au berceau de Seventeen ou Bust en 2002. Depuis novembre 2016, il n'en reste que 5, les 12 autres se sont avérés ne pas être un nombre de Sierpinsky, comme en témoigne le nombre premier de Proth associé à côté d'eux.