Tant qu'un réseau est suffisamment grand, une structure émergera toujours. La mathématicienne Ann Dooms (VUB) explique la "théorie de Ramsey" sur la base de six profils Facebook aléatoires.
Les mathématiciens aiment la structure. Il y a ceux qui étudient des structures spécifiques, tandis que d'autres essaient d'établir des liens entre différentes structures. D'autres encore recherchent une structure là où à première vue il n'y en a pas. L'œuvre de Frank P. Ramsey (1903-1930) appartient à cette dernière catégorie. Le Britannique n'en était peut-être pas conscient lui-même, mais ses résultats ont inauguré un nouveau domaine de recherche, une discipline qui occupe les mathématiciens depuis près de cent ans.
Ramsey, qui a suivi une formation de mathématicien, était à l'aise dans divers domaines :il a travaillé en économie et en philosophie, entre autres. Au King's College de Cambridge, il a collaboré avec le célèbre économiste John Maynard Keynes et le philosophe Ludwig Wittgenstein. Des années plus tard, ses publications sont considérées comme des œuvres influentes d'une importance fondamentale.
Toutes ces réalisations surprenantes détournent l'attention d'un petit résultat auxiliaire dans un travail mathématique sur la logique. C'est un résultat remarquable, qui a conduit au terme de « théorie de Ramsey ». Les scientifiques parlent aussi de la recherche de l'ordre dans le chaos.
L'idée est plus facile à illustrer en termes de réseaux, tels que les réseaux sociaux que vous trouvez sur Facebook. Choisissez six personnes sur Facebook. Ces individus peuvent ou non être amis les uns avec les autres à l'avance. Dans tous les cas, vous avez toujours soit un groupe d'au moins trois personnes qui sont amis, soit un groupe d'au moins trois personnes qui ne sont pas amis.
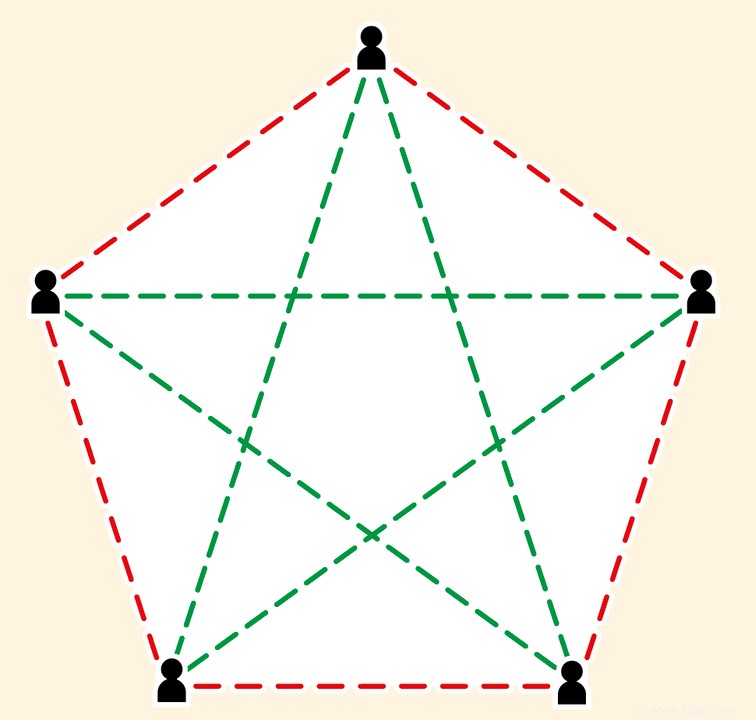
Les lignes vertes pointent vers les amis, les rouges vers les étrangers. Chaque triangle a soit deux lignes rouges et une verte, soit une rouge et deux vertes.
Nous avons trouvé une structure dans cette sélection aléatoire de six profils :un groupe d'amis, ou un groupe d'inconnus. Si nous n'avions choisi que cinq personnes, ce phénomène ne se serait pas produit. L'idée sous-jacente est que tant que le réseau est suffisamment grand, la structure émergera toujours. Ils ne doivent pas toujours être des amis ou des étrangers. Elle peut également impliquer d'autres structures plus complexes.
La théorie a des implications considérables. Dans l'exemple avec Facebook, il semble logique de rechercher des groupes d'amis ou d'inconnus plus importants. Par exemple, combien de profils faut-il choisir pour être assuré de trouver un groupe de quatre amis ou quatre inconnus ? Et si on faisait ça pour n'importe quelle taille n aimerait savoir? C'est exactement comme ça que le nombre de Ramsey R(n) peut être défini. C'est le nombre minimum de profils que nous devons choisir pour trouver avec certitude un groupe de n amis ou n inconnus.
Comme nous l'avons vu, R(3) =6. Avec un peu plus de travail vous pouvez montrer que R(4) =18. A partir de n =5 cela devient une toute autre histoire, car à ce jour la valeur exacte est de R( 5) inconnu. Pour vous donner une idée, en 1997, des experts ont pu montrer que R(5) ≤ 49. Ce n'est que vingt ans plus tard qu'ils ont pu prouver que R(5) ≤ 48. À l'inverse, on sait que 43 ≤ R(5), et certains les experts sont convaincus qu'en effet R(5) =43. Au rythme actuel, on peut s'attendre à une preuve concluante en l'an 2117.
'Si les extraterrestres demandent la valeur de R(6), nous devons les détruire' le mathématicien Paul Erdős
Le progrès scientifique s'accélère bien sûr. Espérons que nous pouvons nous attendre à une solution au cours de ce siècle. Peut-être que ce problème s'avère même être votre solution pour les supercalculateurs de demain. Bien que ce soit moins probable que vous ne le pensez. Si vous voulez montrer par force brute que R(5) ≤ 43, l'ordinateur devrait passer par environ 10 cas. C'est une quantité qui éclipse le nombre d'atomes dans l'univers.
Ou comme l'a dit Paul Erdős, l'un des plus grands mathématiciens du siècle dernier, selon un collègue :« Imaginez une forme de vie extraterrestre bien plus avancée que nous. Les extraterrestres atterrissent sur Terre et nous présentent un choix :donner la valeur exacte de R(5) ou subir une extermination globale. Dans ce cas, tous les ordinateurs et tous les mathématiciens du monde doivent être réclamés et ils doivent essayer de trouver la valeur ensemble. Mais si les extraterrestres demandent la valeur de R(6) à la place, alors nous devrions essayer de détruire les extraterrestres."