Début mars, des "modèles mathématiques" de la pandémie de Covid-19 prédisaient un effondrement de notre système de santé. Le résultat a été un verrouillage pour éviter ce scénario. Le mathématicien Bert Mortier évalue la valeur prédictive de ces modèles mathématiques dans cet article de blog.
En réponse à ces prévisions et aux développements dans des pays comme l'Italie, les gouvernements du monde entier ont eu recours à un confinement strict. Un exemple d'une telle prédiction par un modèle mathématique est illustré dans la figure ci-dessus. Sans confinement, notre système de santé serait débordé.
Étant donné que les modèles mathématiques aident à déterminer la politique, il est indispensable de comprendre comment un modèle mathématique peut être utilisé. Pour cette raison, dans ce texte, nous examinons le modèle mathématique le plus largement utilisé pour la propagation des maladies infectieuses. Nous appliquons ensuite ce modèle à la situation spécifique de la Belgique. Ce modèle mathématique peut ensuite être utilisé pour regarder encore plus loin dans le futur et prédire ce qui se passerait si le confinement devait soudainement prendre fin.
Le nouveau virus SARS-CoV-2 s'installe dans le système respiratoire, où il peut se multiplier aux dépens de l'hôte. Les dommages au système respiratoire des personnes infectées entraînent parfois une maladie grave, le COVID-19, mais généralement une personne infectée se rétablit, après quoi elle devient immunisée. Pendant la période infectieuse, les nombreuses particules virales présentes dans le système respiratoire d'une personne infectée peuvent passer dans de nouveaux individus encore sensibles en voyageant avec des gouttelettes dans l'haleine de la personne infectée. Là, le virus peut alors se multiplier davantage. L'épidémie se déroule ensuite à travers une longue chaîne de contacts en constante expansion qui entraîne de nouvelles infections.
Le modèle mathématique le plus utilisé pour les épidémies simplifie considérablement la réalité. Au lieu de contacts réels entre personnes, le contact entre personnes est modélisé comme s'il y avait une chance égale de contact entre deux personnes. En cas de contact entre une personne infectée et une personne sensible, il y a à nouveau un risque que l'infection se transmette. Le processus de guérison est décrit dans ce modèle comme une chance fixe par jour de guérir.
La description ci-dessus du modèle peut être traduite en équations mathématiques qui indiquent comment le nombre d'individus encore sensibles, noté V , le nombre de personnes infectées, indiqué par B et le nombre de personnes guéries et désormais immunisées, noté I , changer. Ces chiffres changent au fur et à mesure que les personnes sensibles sont infectées par contact avec d'autres personnes infectées et que les personnes infectées se rétablissent. Ces changements sont illustrés dans la figure ci-dessous.

Le modèle décrit ces changements par, pour chacun de ces trois groupes de personnes, le nombre de personnes dans ce groupe sur le n -représenter le jour par B n , V n et je n † Le modèle décrit ensuite le nombre d'individus infectés, sensibles et immunisés sur les éléments suivants, (n+1) -e, jour basé sur les chiffres du n -journée. Pour décrire cette évolution, la probabilité de contact entre deux personnes, κ , le risque d'infection en cas de contact entre une personne sensible et une personne infectée, α et les chances de guérison par jour, γ , nécessaire. Avec ces probabilités, le nombre de nouvelles infections et le nombre de personnes guéries peuvent être exprimés mathématiquement. Comment cela fonctionne exactement est expliqué dans la boîte grise pour les personnes intéressées. Ces changements sont représentés mathématiquement dans la figure ci-dessous.

Cela permet d'établir les équations mathématiques pour le nombre d'individus infectés, sensibles et immunisés sur le (n+1) -eh, jour. Ce sont :
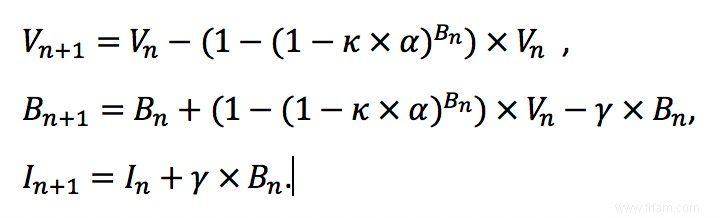

Les équations ci-dessus peuvent représenter l'évolution du nombre d'individus sensibles, infectés et immunisés, mais avant de les utiliser, nous avons besoin de valeurs pour V , B et je un jour donné, ainsi que des valeurs pour les cotes κ , et γ † Des estimations de ces probabilités étaient disponibles très tôt dans l'épidémie, à savoir γ=1/13 , κ×α= 3,7 × 10 † Nous pouvons expérimenter ces valeurs. Par exemple, on peut essayer de regarder comment le nombre d'infections évoluerait en Belgique, avec une population de 11.500.000 personnes, à partir d'une seule infection. Cela signifie B 1 =1 , V 1 =11 499 999 et je 1 =0 † Brancher ces valeurs dans les équations donne une prédiction de B 2 , V 2 et je 2 † L'insertion de ces nouvelles valeurs dans les équations donne à nouveau B 3 , V 3 et je 3 † Ce processus peut être poursuivi jusqu'à ce que nous obtenions les valeurs B 365 , V 365 et je 365 peut calculer, un an après l'apparition de la première infection.
Le résultat de ce processus est illustré dans la figure ci-dessous. Cela nous indique que l'épidémie peut commencer lentement, mais après quelques mois, des millions de personnes seraient infectées en même temps.
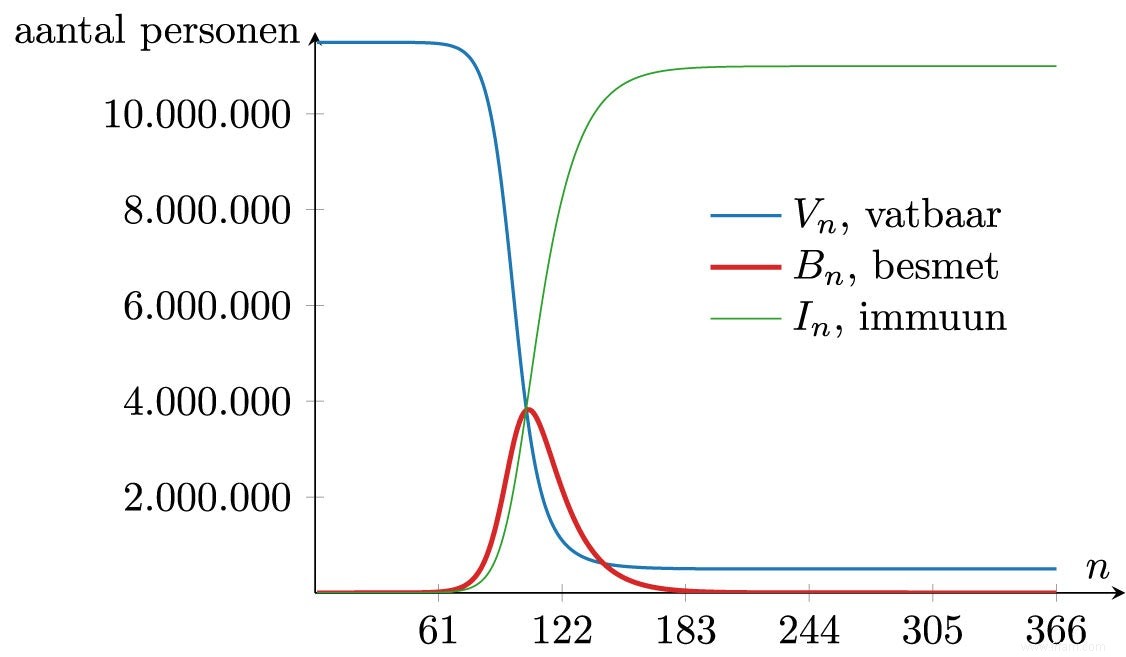
La question est maintenant de savoir si c'est un problème. Une première comparaison a suggéré que la nouvelle maladie n'est pas beaucoup plus nocive que la grippe, mais elle est beaucoup plus contagieuse. Cette comparaison rend logique de laisser proliférer la maladie dans une mesure limitée, sans arrêter nos vies. Au fil du temps, cependant, il est devenu clair que l'impact du nouveau coronavirus est beaucoup plus important. Il a fallu attendre les développements dramatiques dans le nord de l'Italie pour que des mesures drastiques soient prises dans toute l'Europe pour contenir l'épidémie. L'impact du virus sur notre société peut être intégré dans le modèle mathématique, par exemple en modélisant le nombre de lits de réanimation pris. Nous indiquons le nombre de lits en soins intensifs (USI) avec Z † Des données disponibles indiquent qu'environ 0,82 % des personnes infectées ont besoin d'un lit de soins intensifs. Nous pouvons décrire cela mathématiquement en déclarant que
Z n =0.0082 ×B n .
L'évolution du nombre de lits IZ requis peut être facilement trouvée dans la figure précédente. Cette évolution est illustrée dans la figure ci-dessous. La ligne noire indique la capacité maximale de lits en soins intensifs en Belgique. Ce graphique illustre très clairement qu'un désastre se produirait si le virus ne pouvait pas être contenu.
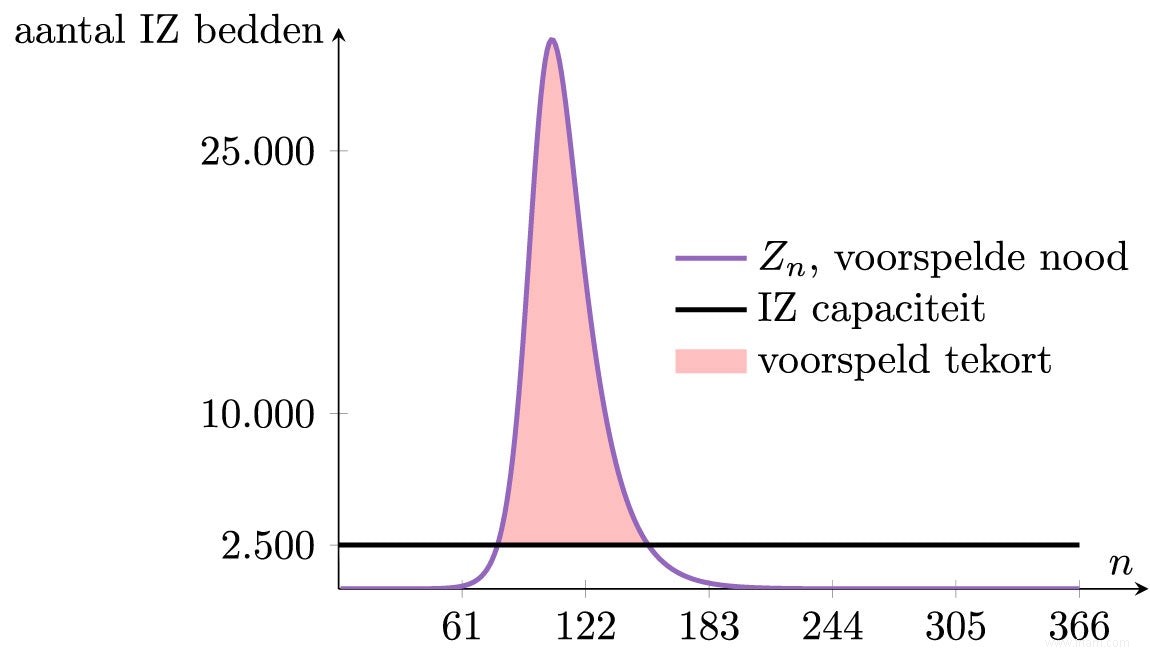
Un tel résultat du modèle appelle une action très importante. Cependant, cela n'est clair qu'après que le lourd impact sur les soins de santé a également été inclus dans le modèle. Cela ne doit pas être perdu de vue lors de la modélisation :si la cause correcte n'est pas incluse, les conclusions peuvent ne pas être correctes. Un deuxième aspect est que les prédictions faites par le modèle ne contiennent pas plus de détails et de précision que le modèle lui-même. Ainsi, la forme de contact modélisée est une agrégation très simpliste de la réalité, et les prédictions ne seront donc pas très précises. Tout ce que le modèle peut faire, c'est prédire approximativement comment l'épidémie dans son ensemble évoluerait. Outre les simplifications considérables du modèle, la précision est également compromise car les valeurs de κ , α et γ déterminé à partir des données limitées disponibles.
Même si le modèle est loin et que le nombre maximum de lits de soins intensifs requis n'est pas de 30 000, mais "seulement" de 10 000, la conclusion est toujours d'actualité :si rien ne changeait, notre système de santé serait débordé.
Nous pouvons utiliser le modèle mathématique ci-dessus pour faire des prédictions générales grâce aux données de l'étranger sur la maladie et sa propagation. Ces données ont été utilisées pour calculer les valeurs de κ , α et γ decider. La manière exacte dont la pandémie a progressé en Belgique diffère des hypothèses formulées ci-dessus. Ce n'était pas le cas que l'épidémie en Belgique ait commencé avec 1 personne infectée, et le confinement introduit a également fait une énorme différence.
Nous pouvons établir un lien entre le modèle mathématique simple et la réalité belge sur la base de trois éléments. Premièrement, il y a un nombre initial d'infections à partir duquel le point de départ est fait, par exemple le nombre au 1er mars. Deuxièmement, il y a la mesure dans laquelle le nombre de contacts et le risque de contamination lors de ces contacts ont diminué après le confinement. Cela détermine un changement de κ×α depuis le confinement. Enfin, il y a eu une période d'ajustement, au cours de laquelle l'effet des mesures est progressivement devenu visible. Ces trois choses se résument en trois chiffres :B 1 est le nombre de personnes infectées au 1er mars β est le facteur par lequel κ×α a refusé et T est le temps d'ajustement après lequel l'effet des mesures était vraiment complet.
Ces trois nombres, B 1 , β et T sont inconnues, et nous les choisirons pour que le modèle corresponde à la réalité belge. Cela se fait via un ajustement dit de modèle. Il s'avère que le meilleur choix est qu'il y a eu 1 000 infections le 1er mars (B 1 =1 000) , que le confinement a réduit d'un facteur 8 le nombre de contacts et les transferts qui en résultent (β=8 ), et qu'il a fallu environ 30 jours pour que l'effet soit complet (T=30 † Avec ces choix, le résultat du nombre prévu de lits de soins intensifs occupés correspond très bien à la réalité belge.
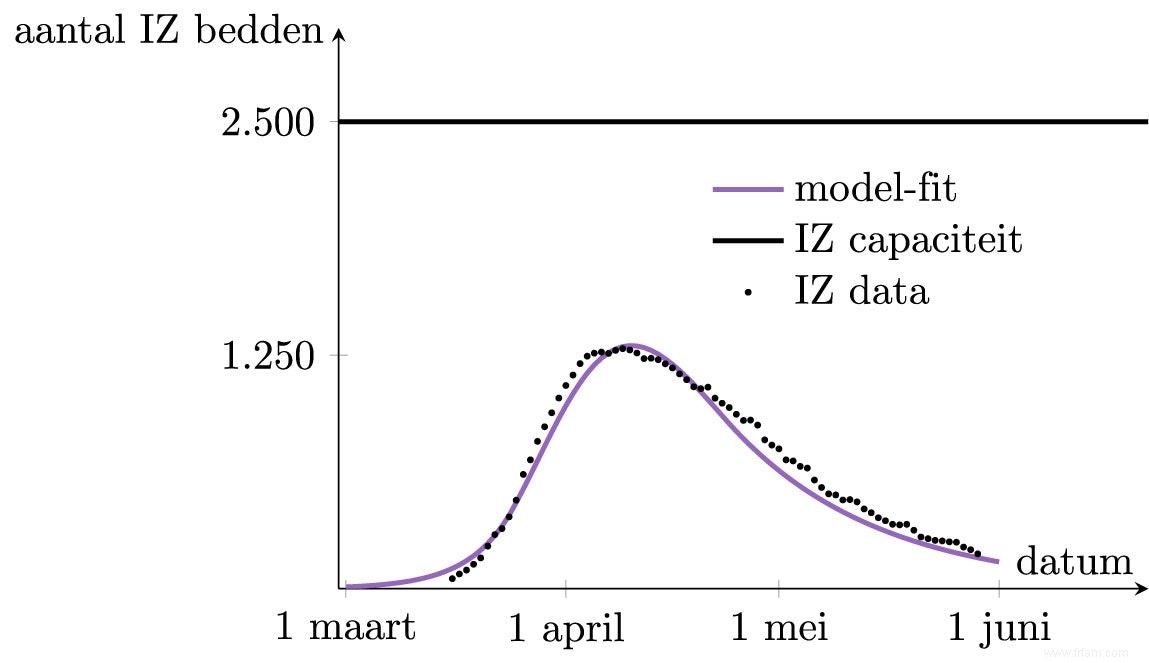
Nous avions déjà un modèle, mais maintenant nous avons aussi un modèle qui « marche » pour la Belgique. Nous pouvons maintenant faire de nouvelles prédictions sur l'évolution de l'épidémie en Belgique.
Par exemple, nous pouvons utiliser le modèle mathématique pour prédire ce qui se passerait en Belgique si toutes les mesures devaient se terminer le 1er juin. Cela peut être inclus dans le modèle mathématique en ajoutant les valeurs de κ à partir du 1er juin. , α et γ revenir aux valeurs d'origine. Le résultat peut être vu ci-dessous, et ce serait encore un désastre. Cette prédiction montre donc qu'une levée complète des mesures n'est pas possible tant qu'il n'y aura pas de vaccin ou d'immunité plus large. Cependant, l'hypothèse selon laquelle toutes les mesures ont été levées le 1er juin en Belgique n'est pas tout à fait correcte. Par exemple, il y a toujours des restrictions sur les rassemblements en grands groupes tout au long de l'été, les grands événements ont été abolis presque partout et les masques buccaux sont obligatoires à plusieurs endroits. Il faut donc s'attendre à ce que l'augmentation de la réalité ne soit pas aussi extrême que dans le graphique ci-dessous.

Il reste à voir quelle sera l'ampleur de l'effet de toutes ces mesures restantes. Notez également qu'il peut y avoir un certain délai entre la levée des mesures et l'apparition d'une augmentation du graphique. Dans l'exemple ci-dessus, où le verrouillage a été complètement levé le 1er juin, il faudra attendre la mi-août pour que la demande de lits de soins intensifs augmente à nouveau clairement. Cependant, une fois qu'il commencera à augmenter, il ne faudra pas longtemps avant que la situation redevienne précaire. Il est donc possible qu'un nouveau confinement soit nécessaire très soudainement.
La précision des prédictions du modèle mathématique dépend toujours de l'examen du marc de café. Il y a une énorme différence entre l'ajustement du modèle avec les données IZ belges, qui étaient presque parfaites, et les prévisions futures de ce qui se passerait s'il n'y avait plus de verrouillage. Le grand accord entre les données IZ et le modèle provient du fait que les valeurs B 1 , β et T être choisi de manière à ce que la courbe s'ajuste bien. Pour les valeurs futures, cette astuce ne peut pas être utilisée et la précision des prédictions futures dépend donc de la précision du modèle, qui est incertaine. Pour le dire franchement :les modèles sont particulièrement efficaces pour prédire dans le passé, et beaucoup moins dans le futur.
S'il y a des erreurs dans les prédictions, le modèle peut être affiné, par exemple en prenant en compte des effets supplémentaires. Par exemple, on peut tenir compte du fait que le virus se propage mieux ou moins bien selon la météo, ou les contacts humains peuvent être mieux décrits dans le modèle mathématique. En réalité, nos contacts ne sont pas totalement aléatoires :nous entrons plus souvent en contact avec des personnes qui habitent à proximité, ou travaillent au même endroit, etc. Tous ces aspects supplémentaires peuvent être capturés dans de nouveaux modèles mathématiques. Pour que ces aspects soient représentés avec précision, des données seront nécessaires. Par exemple, des données sont nécessaires sur le nombre moyen de contacts avec les voisins, les collègues et la famille, et sur l'ampleur du risque d'infection dans ces différents types de contacts. S'il existe des données fiables pour déterminer ces données, le modèle mathématique peut fournir des prédictions de mieux en mieux.