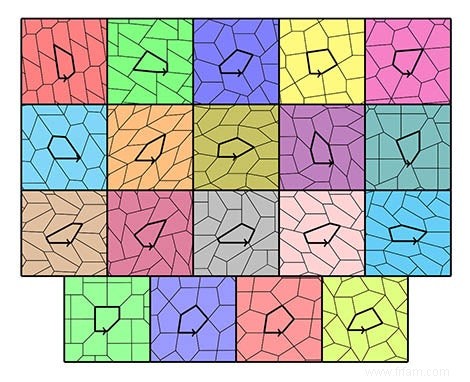
Les mathématiciens n'ont pas besoin de chercher plus loin :il n'y a que quinze pentagones différents avec lesquels un plan peut être complètement rempli.
Vous pouvez utiliser toutes sortes de polygones dans une mosaïque, mais les artistes optent généralement pour un motif fixe ou une symétrie. Juste des triangles, par exemple, ou une alternance de pentagones et d'hexagones - ce dernier motif peut également être trouvé sur un ballon de football. Il est connu pour les triangles et les quadrilatères que vous pouvez remplir complètement une surface avec une seule et même copie - il n'y a pas un grain d'espace entre les carreaux. Cela a déjà été démontré en 1918 par le mathématicien allemand Karl Reinhardt, qui a simultanément prouvé qu'il n'y a que trois hexagones capables de faire cela, et pas un seul heptagone.
La question du pentagone « flat-filling » restait ouverte. De temps en temps, un mathématicien pouvait trouver un pentagone bien défini, de sorte que la liste s'allongeait régulièrement. En 2015, le compteur a bondi à 15 – entre le numéro 14 et 15, ce n'était pas moins de trente ans. Il y a deux ans, la question était de savoir si cette liste était complète. Oui, comme le montrent désormais les travaux de Michaël Rao, mathématicien français.
Rao a écrit un programme avec lequel il pouvait générer tous les pentagones de remplissage de surface possibles - prouvant ainsi immédiatement que ce nombre est fini. Il est arrivé à 371 « familles » de candidats, dont 19 sont finalement restées. Pendant un moment, le mathématicien a pensé qu'il avait découvert quatre nouveaux pentagones remplissant une zone, mais en y regardant de plus près, ces quatre copies se sont avérées être des variantes spéciales des quinze pentagones existants.
Les quinze pentagones remplissent périodiquement le plan bidimensionnel "plat". On ne sait pas s'il existe également des pentagones qui le font de manière apériodique.